Dit klinkt meer als een wiskunde opgave voor me.

waarbij je eerst moet doorhebben dat die ronde bal ook geschreven kan worden als

(x-1)² + (y+1)² + z² = 7

door gebruik van kwadratische producten zoals voor x:

(x² - 2x) = (x² - 2x +1)-1 = (x-1)² -1

Dus de bal bevindt zich met middelpunt in (1,-1,0) en straal √7

Punt P (10,2,5) kan op vele manieren dan een vlak voor P en rustend op de bal tekenen, wat een cirkel oplevert (feitelijk vormen cirkel op de bal en punt P een pyloon).

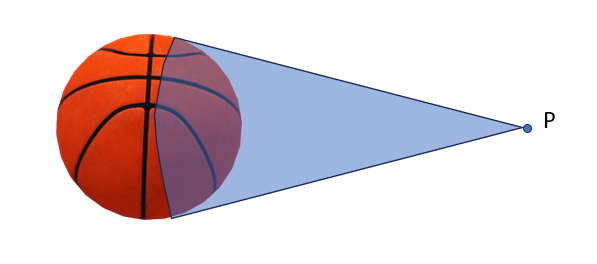
Hoe die cirkel een eenparig rechtlijnige beweging geeft is mij niet duidelijk. Niks in een cirkelbeweging is eenparig rechtlijnig. Bij geschikte middelpuntzoekende versnelling (of kracht) wel eenparig (gelijkblijvende) snelheid als grootte (getalwaarde "speed") langs de cirkel, maar wel voortdurend van richting veranderend als vector ("velocity").

Dag Tobias,
Kun je de vraagstelling verduidelijken?
a. Moet je de meetkundige vergelijking opstellen van een cirkel op het oppervlak van de basketbal zodanig dat elk punt van de cirkel een punt is waar een vlak door P de basketbal raakt?
b. Wat is dan bedoeld met 'die cirkel waarop een eenparige rechtlijninge beweging opwerkt'? Welk ding zal die eenparige rechtlijnige beweging uitvoeren? Is dat een ding op de cirkel? Onder invloed van welke krachten? Heffen die krachten elkaar op, omdat een eenparige rechtlijnige beweging anders niet optreedt?
c. Waar op aarde bevindt zich het middelpunt van de basketbal? Zijn $x$, $y$, $z$ en de straal van de basketbal in de eenheid meter?
Groet, Jaap

Dag Theo,
Je zegt 'feitelijk vormen cirkel op de bal en punt P een pyloon'.
'Pyloon' snap ik in deze situatie niet.
Bedoel je dat het blauwe oppervlak in je figuur de mantel is van een kegel met top P?
https://nl.wikipedia.org/wiki/Kegel_(ruimtelijke_figuur)
Groet, Jaap

Inderdaad kegel - ik kwam even niet op het woord.

Theo

Dag Jaap, mijn boek vraagt om de vergelijking van de cirkel te vinden (ik denk dat je dan eigenlijk de doorsnede van de basketbal (bol) en een vlak moet zoeken, maar dan heb je nog een normaalvector nodig). Deze vraag komt uit een fysica boek, maar ik vind het ook vreemd dat het zo wiskundig is. Als de vglk van de cirkel hebt ik denk door een stelsel van enerzijds de vglk van de bol (basketbal) en ene vlak hebt, dan moet je de straal zoeken en de frequentie zoeken, want 'een voorwerp' gaat in 1 min een keer rond die cirkel.

>een voorwerp' gaat in 1 min een keer rond die cirkel

Dus niks eenparig rechtlijnig.

De rest uitrekenen is vooral wiskunde: rechthoekige driehoek met scherpe punt P, rechte hoek op verbinding P-bal middelpunt. ChatGPT kan het ongetwijfeld voorrekenen (wel controleren op onzin!).

Dag Tobias,
Omdat in de opgave staat 'alle raakvlakken uit P op de bol', snap ik nog niet dat je, zoals je zegt, eigenlijk de doorsnede van de basketbal en een [=1, een enkel?] vlak moet zoeken'.

Voorlopig neem ik aan dat je de vergelijking moet opstellen van een cirkel op het oppervlak van de basketbal zodanig dat elk punt van de cirkel een punt is waar een vlak door P de basketbal raakt. In Theo's figuur is dat de cirkel waar de kegelmantel de bol raakt.

Mijn eerste idee: stel de vergelijking op van een rechte met parameters $a$, $b$ en $c$.


Eis dat P op de rechte ligt:


Eis dat de rechte de bol snijdt in 1 of 2 punten:


Uit (1) en (2) kunnen we $c$ elimineren. We vinden dan een vergelijking (3), kwadratisch in $x$, kwadratisch in $y$, met de parameters $a$ en $b$.

'Raken' veronderstelt het samenvallen van de twee mogelijke snijpunten van de rechte en de bol. Kunnen we dit schrijven als een voorwaarde (4) voor de discriminant $D=0$ van een kwadratische vergelijking?
Kunnen we de waarde van $a$ en $b$ vinden door combinatie van (3) en (4)? Dan zijn we al een stap op weg naar de gevraagde vergelijking van de cirkel.

Maar dan is me nog niet duidelijk wat bedoeld wordt met 'die cirkel waarop een eenparige rechtlijnige beweging opwerkt'.
Je schrijft dat een voorwerp 'gaat in 1 min een keer rond die cirkel.' Dat lees ik niet in de opgave. Hoe zit dat?
Groet, Jaap