dag Lucas,

1) we halen het touw even weg en jij duwt dat gewicht met 100 N naar boven. 

- hoe groot is de kracht van je hand op dat gewicht ? (duhh) 
- wat gebeurt er met dat gewicht? 
- als je denkt dat de groottes van de krachten trekkend met dat touw ertussen echt anders zal zijn, probeer dan eens uit te leggen waarom? 

2) is een zelfde gevalletje als 1). kantel de hele situatie 90 graden, bedenk een persoon met een gewicht van 900 N die hangend aan een touw met een kracht van 1000 N omhoog wordt getrokken. 

Groet, Jan

Hi Jan,

Ik zou zelf zeggen in de eerste situatie 100N, 90N om hem stil te houden en 10N om te versnellen. Dus ik vermoed dat de spankracht in het touw 100N moet zijn. In de 2e situatie eigenlijk hetzelfde: Met 900N trek je even hard, dus touw blijft stil, maar met 1000N komt het touw in beweging. Dus spankracht in het touw 1000N lijkt me.

Maar als ik dit aan Perplexety vraag, dan zegt hij in de eerste situatie 100N en in de 2e situatie 900N. En dat snap ik niet. Nu vertrouw ik AI apps niet blindelings, dus vandaar mijn vraag hier.

Hij zegt dat in de 2e situatie de spankracht altijd gelijk is aan de kant waar met de minste kracht getrokken wordt. Maar in de eerste situatie geeft hij weer aan de grootste kracht van die 2...

Bij nader inzien denk ik eigenlijk dat het voor beide situaties de minste kracht is. On het gewicht omhoog te houden heb je 90N nodig, die 10N extra is om te versnellen. De spankracht in het touw zal denk ik gewoon 90N blijven, tijdelijk iets hoger door inertie van het gewicht. In de andere situatie volgens mij precies hetzelfde. Bij 900N is het touw in stilstand. Maar trekt de ene persoon met 1000N dan wordt deze 100N extra gebruikt voor beweging en de overige 900N moet dan de spankracht in het touw zijn.

Ik ben benieuwd naar het juiste antwoord.

Mvg

Lucas

dag Lucas,

Je redenering spreekt zichzelf een beetje tegen :) 
Als die 100 N extra wordt gebruikt voor beweging (versnelling) zoals je terecht opmerkt, dan zal die 100 N toch ook op een of andere wijze van de trekker  bij het getrokkene moeten raken. Een andere weg dan via dat touw zie ik niet. 

Kortom, 1000 N spankracht, 900 om een tegenkracht te compenseren, schiet er netto 100 N over voor versnelling a=F_netto/m 
Groet, Jan

Dag Jan,
Ik vul je reactie van 01 november om 09.19 uur cursief aan zoals ik denk dat je het bedoelt.
1) - hoe groot is de kracht van je hand op dat gewicht? 100 N
- wat gebeurt er met dat gewicht? Het krijgt een versnelling omhoog en gaat versneld omhoog bewegen als het aanvankelijk in rust was.
- als je denkt dat de groottes van de krachten trekkend met dat touw ertussen echt anders zal zijn, probeer dan eens uit te leggen waarom?
niet anders. conclusie: de spankracht is 100 N.
2) is een zelfde gevalletje als 1). kantel de hele situatie 90 graden, bedenk een persoon met een gewicht van 900 N die hangend aan een touw met een kracht van 1000 N omhoog wordt getrokken.
Volgens de redenering van geval 1: de hangende persoon krijgt een versnelling omhoog, conclusie: de spankracht is 1000 N.
Is dit inderdaad de redenering die je voor ogen staat en is de spankracht volgens jou 100 N respectievelijk 1000 N?

Dag Lucas, wordt vervolgd...
Groet, Jaap

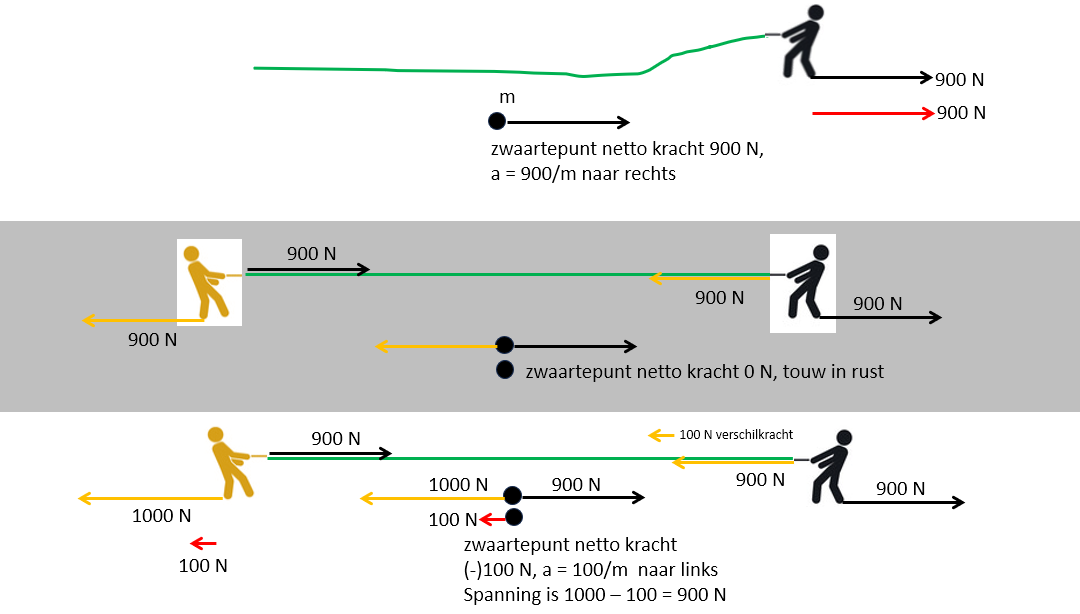
Een gewicht met massa 1kg weegt 10 N (=zwaartekracht). Om het bewegingsloos aan een touw te laten hangen moet het touw een tegenkracht van 10 N leveren: de spanning in het touw.

Als aan het touw met 100 N getrokken wordt, dan is 10 N nodig ter compensatie van het gewicht, de rest resulteert in een versnelling behorend bij een kracht van 90 N.  Aangezien elk deel van het touw dezelfde versnelling ondergaat is de spanning overal gelijk: 90 N. 

Voor touwtrekken kun je volgende redenering houden. Neem aan dat links met 1000 N en rechts met 900 N trekt. Uit ervaring weet je dat links dan wint en het touw naar links beweegt. Neem voor de richting aan dat naar links negatief is (zoals in de wiskunde gebruikelijk)

1. Bekijk een stukje touw (of neem het zwaartepunt als vertegenwoordiger van het hele touw). Alle delen bewegen dezelfde kant op met dezelfde snelheid en versnelling. Zo niet zou het touw knappen. 
2. Op zo'n stukje touw werken twee krachten, afkomstig van de trekkers aan beide uiteinden. De resultante is de kracht waarmee het stukje touw zal bewegen. In het voorbeeld -1000 + 900 = -100 N naar links.
3. Dat betekent dat de spanning de kleinste van de twee trekkrachten is: 900 N. Trekken beide kanten even hard, dan staat het touw stil (Netto kracht 0 N) en is de spanning in het touw aan beide uiteinden 900 N maar tegengesteld.
4. Bij ongelijke trekkracht is er een netto kracht die bepaalt hoe snel en in welke richting de beweging is. De rest is de spanning, die naar beide kanten toe gelijk is (bij alleen spanning beweegt het touw niet: netto kracht 0 N)
    In het voorbeeld is er een netto kracht -1000 +900 = -100 N naar links ervaart. De spanning is 990 N. De rechter persoon trekt met +900 N, de spanning - 900 N en deze  heffen elkaar op. Maar het hele touw (en alles wat eraan vast zit) beweegt door een kracht van -100 N naar links.
   De linker persoon ervaart een spanning van +900 N en trekt (de grond doet dit als reactiekracht) met -1000 N zodat de persoon beweegt door een kracht = -1000+900 = -100 N
5. Alles, linker en rechter persoon en touw, beweegt door een kracht van -100 N

"Als die 100 N extra wordt gebruikt voor beweging (versnelling) zoals je terecht opmerkt, dan zal die 100 N toch ook op een of andere wijze van de trekker  bij het getrokkene moeten raken. Een andere weg dan via dat touw zie ik niet."

Ja, als je het zo zegt, klinkt het wel logisch, ja. Ik moet jullie eerlijk bekennen dat ik deze materie sowieso een beetje verwarrend vind. 
Toen ik voor het eerst de vraag kreeg: 'Er wordt aan 2 kanten met 100N getrokken, welke spankracht ontstaat er in het touw?' dacht ik dat dit 200N moest zijn. En ik krijg nog altijd niet helemaal helder waarom dit niet zo is. Als ik me dan bedenk dat het touw aan een muur zit en ik met 100N aan het touw trek, dan vind ik het weer wel logisch; mijn denkbeeldige newtonmeter geeft 100N aan, de muur moet wel met 100N terugtrekken anders zou het touw bewegen. Vervang ik de muur voor iemand die met 100N terugtrekt dan heb je eigenlijk dezelfde situatie. Maar dan denk ik weer... huh... er wordt toch met 100N teruggetrokken?? :)

Maar het klinkt eigenlijk wel logisch dat als er met 1000N aan het touw getrokken wordt, dit natuurlijk ook allemaal via het touw doorgegeven moet worden. Dus als de 'weerstand' 900N is, dan wordt er 100N voor de acceleratie gebruikt en is de spankracht in het touw 1000N. 

De reactie van Theo hierboven mij lijkt dit dan weer tegen te spreken??

Theo, bedankt voor je afbeelding en uitleg.
Betekent dit, dat ik met mijn reactie van 02 november 2025 om 16:26 toch goed zat?

En begrijp ik dat je zelf dan een klein foutje maakt in je reactie van 02 november 2025 om 19:18?
Want je zegt dat de spankracht in die situatie 90N moet zijn. Maar als ik je uitleg goed begrijp, dan zou dit 10N moeten zijn? Want de rest wordt gebruikt voor acceleratie?

Je hebt gelijk - 10 N spanning, 90 N om te versnellen. Ben ik toch weer in de valkuil getrapt.

Dag allen,
Er zijn verschillende antwoorden gegeven op Lucas' twee vragen.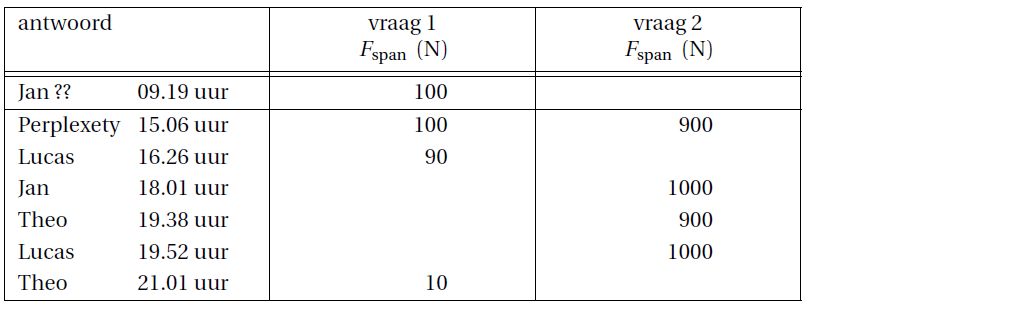

Wat zouden nu de juiste antwoorden zijn?
Groet, Jaap

Ik hoop zelf die van Theo :)

Want dan krijg ik het verhaal een beetje kloppend in mijn hoofd. Ik zie het zo: Stel ik heb een touw met daaraan een weegschaal en weer een stuk touw met daaraan een zwaar gewicht op een vlakke ondergrond. Pas wanneer ik met 1000N trek komt het gewicht pas in beweging en gaat schuiven. Mijn weegschaal geeft 100kg aan. Nu ga ik versnellen en trek ik met 1100N. Ik vermoed dat mijn weegschaal nog altijd 100kg aangeeft. Want de wrijving vraagt 1000N aan kracht en de 100N extra is voor het accelereren.

En ik denk dat het niet uitmaakt of deze 'tegenkracht' nu van de zwaartekracht is, mensen die aan een touw trekken of een andere vorm van weerstand is.

Dag allen,
Lucas' vraag 1 kunnen we met de redenering van Jan van 01.11.2025 om 09.19 uur beantwoorden: de spankracht van het touw is $100\,\text{N}$. Dat lijkt me juist.

Jan schrijft '2) is een zelfde gevalletje als 1)'. De redenering van vraag 1 brengt Jan om 18.01 uur bij vraag 2 tot een spankracht van $1000\,\text{N}$. Dit is mijns inziens niet juist.
Daarom gebruik ik bij vraag 1 een andere aanpak, die ook toepasbaar is bij vraag 2.

Noem de massa van 'het gewicht' $M=1\,\text{kg}$ en de massa van het touw $m$.
De zwaartekracht op het gewicht en het touw samen is $(M+m)\cdot 10$.
De resulterende kracht op het gewicht en het touw samen is

Hierdoor krijgen het gewicht en het touw een versnelling

Als we een touw kiezen met $m\ll 1\,\text{kg}$, is de versnelling bij benadering

Op het gewicht is nodig een omhoog gerichte resulterende kracht

Deze resulterende kracht bestaat uit de 'spankracht van het touw op het gewicht' omhoog en de 'zwaartekracht op het gewicht' omlaag.
De spankracht van het touw is dus $90+10=100\,\text{N}$.
Laten we eens zien waar deze aanpak toe leidt bij Lucas' vraag 2.
Groet, Jaap

Dag allen,
Voor Lucas' vraag 2 gebruik ik dezelfde aanpak als bij vraag 1.
Opnieuw noem ik de massa van het touw $m$.
De resulterende kracht op het touw is $F_\text{res}=1000-900=100\,\text{N}$.
Hierdoor krijgt het touw een versnelling $a=F_\text{res}/m=100/m$.
Wat de resulterende kracht doet, is aan het touw een versnelling geven. De resulterende kracht bepaalt niet de grootte van de spankracht van het touw. 
De spankracht wordt enkel en alleen bepaald:
• door de volledige $900\,\text{N}$ waarmee de ene persoon trekt en
• door $900\,\text{N}$ van in totaal $1000\,\text{N}$ waarmee de andere persoon trekt.
De spankracht van het touw is $900\,\text{N}$.

Het touw kan niet massaloos zijn. De resulterende kracht zou aan een massaloos touw een versnelling $a=F_\text{res}/m=100/0$ geven. Dit is wiskundig onbepaald en natuurkundig onmogelijk.
Groet, Jaap

dat kan niet anders dan WEL bepalend zijn. 

Inderdaad, maar touwtrekkers ook niet. En zo zal dan de nettokracht het systeem met twee touwtrekkers gaan versnellen, en de spankracht ergens tussen de 900 en 1000 in liggen, verdeeld naar rato van de massa's van beide touwtrekkers.  Dat de winnende touwtrekker ook een massa heeft had ik inderdaad over het hoofd gezien. 

Groet, Jan

Verbeter me als ik het fout heb:

Persoon A trekt met 1000N aan het touw en persoon B trekt met 900N aan het touw. Netto kracht 100N. De spankracht in het touw is de kracht die nodig is om het touw 'op zijn plek' te houden, dus 900N. Maar omdat het touw ook zwaartekracht heeft, is dit iets meer dan 900N (?)
De overige 100N wordt gebruikt om te versnellen.

Ik zie nog even niet waarom dit verandert als we het plaatje 90 graden draaien.
Er hangt een gewicht van 90kg aan een touw, deze ervaart een kracht (afgerond naar boven) van 900N naar de aarde. Nu ga ik met 1000N dit gewicht omhoog trekken. Er was 900N om het gewicht 'op zijn plek' te houden. 100N om te versnellen. Waarom is de spankracht in het touw nu wel 1000N?

>Waarom is de spankracht in het touw nu wel 1000N?

Nu maak jij ook mijn eerdere fout. Spankracht blijft 900 N om het gewicht aan het touw te houden, de resterende 100 N zorgt voor beweging van het geheel. 

Ja, maar jullie lijken het nu niet met elkaar eens te zijn. 

Jij zegt, spankracht in mijn laatste voorbeeld blijft 900N. 

Jaap en Jan lijken te zeggen dat de spankracht gelijk is aan de krachtwaarmee getrokken wordt.

En nu weet ik het niet meer :)

Perplexity geeft ook 2 verschillende antwoorden maar zijn uitleg is te vaag. 

Dit topic is nu echt een zootje aan het worden, door (denk)fouten en misverstanden. Maar anders dan een versie van het toestel van Atwood kan deze kwestie nooit zijn. 

Ik bedenk een elektromotor met verwaarloosbare massa met een massaloos touw rond een as. Die schroef ik aan de aarde vast en laat ik met een kracht van 1000 N aan een touw trekken. 

Aan de andere zijde een persoon met een massa van 80 kg die met een kracht van 800 N aan dat touw trekt. 
Spankracht zal 1000 N zijn. 800 N daarvan heft de trekkracht van de touwtrekker op, 1000-800=200 N is netto over, die de touwtrekker zal versnellen met a=F/m = 200/80 = 2,5 m/s² in de richting van de elektromotor. 

Nu twee touwtrekkers, elk m=80 kg. 
Er is weer een nettokracht van 200 N over in de richting van de sterkste trekker. Beide trekkers gaan bewegen met een versnelling van a=F/m = 200/160 = 1,25 m/s² .
Om de zwakste trekker te versnellen met 1,25 m/s² is F=ma = 80 x 1,25 = 100 N nodig. Spankracht in het touw zal dan 800 + 100 = 900 N zijn. (de resterende 100 N versnelt de sterkste trekker zonder dat het touw daarvoor benodigd is). Alles geheel volgens Atwood. 

Nu twee touwtrekkers, de sterke m=120 kg (en F nog steeds 1000 N) , de verliezer m=40 kg (en F= 800 N)
Er is weer een nettokracht van 200 N over in de richting van de sterkste trekker. Beide trekkers gaan bewegen met een versnelling van a=F/m = 200/160 = 1,25 m/s² .
Om de zwakste trekker te versnellen met 1,25 m/s² is F=ma = 40 x 1,25 = 50 N nodig. Spankracht in het touw zal dan 800 + 50 = 850 N zijn. (de resterende 150 N versnelt de sterkste trekker zonder dat het touw daarvoor benodigd is). Weer alles geheel volgens Atwood. 

Laat ik beide elektromotoren met verwaarloosbare massa (en verwaarloosbare inductieve weerstand zodra het gaat draaien) de trekwedstrijd (800<>1000 N) uitvoeren dan schiet het massaloze touw in een oogwenk weg. Nettokracht 200 N, massa 0,00000000000..... kg , a=F/m = 200/0,00000000..... = enorm veel m/s² 

Groet, Jan

"Ik bedenk een elektromotor met verwaarloosbare massa met een massaloos touw rond een as. Die schroef ik aan de aarde vast en laat ik met een kracht van 1000 N aan een touw trekken. 

Aan de andere zijde een persoon met een massa van 80 kg die met een kracht van 800 N aan dat touw trekt. 
Spankracht zal 1000 N zijn. 800 N daarvan heft de trekkracht van de touwtrekker op, 1000-800=200 N is netto over, die de touwtrekker zal versnellen met a=F/m = 200/80 = 2,5 m/s² in de richting van de elektromotor."

Dit klinkt logisch, dit is mij nu helemaal helder. Met mijn eerste foutieve gedachte dat de spankracht altijd gelijk moest zijn aan de zwaartekracht x massa, zou het touw nooit kunnen knappen als je extreem hard accelereert. In praktijk weet ik dat dit niet zo is. Duidelijk.

"Nu twee touwtrekkers, elk m=80 kg. 
Er is weer een nettokracht van 200 N over in de richting van de sterkste trekker. Beide trekkers gaan bewegen met een versnelling van a=F/m = 200/160 = 1,25 m/s² .
Om de zwakste trekker te versnellen met 1,25 m/s² is F=ma = 80 x 1,25 = 100 N nodig. Spankracht in het touw zal dan 800 + 100 = 900 N zijn. (de resterende 100 N versnelt de sterkste trekker zonder dat het touw daarvoor benodigd is). Alles geheel volgens Atwood."

Dit moet ik nog even laten bezinken. Dus touwtrekker A trekt met 1000N naar links en touwtrekker B trekt met 800N naar rechts. Netto 200N naar links.
Ik zou dan zeggen: Touwtrekker B gaat met 200N/80kg = 2,5m/s² naar links en de spankracht is 1000N?

Nee, want touwtrekker B gaat achteruit bewegen (zo werkt dat bij touwtrekken in tegenstelling tot die elektromotor) en heeft ook een massa die ook versneld moet worden. 
De nettokracht moet beide massa's versnellen. a= F/m = 200/(80+80) =1,25 m/s² 
Om de verliezende touwtrekker te versnellen is F=ma = 80 x 1,25 = 100 N nodig
spankrqacht dus 800 + 100 = 900 N 

Waarschijnlijk terwijl jij typte heb ik mijn verhaal nog uitgebreid met een geval van twee touwtrekkers met ongelijke massa. . 

Ik zie nu dat je het gewicht van touwtrekker A meeneemt in je berekening voor de acceleratie. Maar het touw heeft toch 'geen weet van' het gewicht van touwtrekker A? Waarom moet je die meenemen in het berekenen van de acceleratie?

Dan zie ik touwtrekker A voor me als een elektromotor. Het kan een elektromotor zijn van 500kg of van 1000kg, hij trekt met een kracht van 1000N en zal het gewicht van trekker B versnellen met 200N/80kg?

auto rijdt met caravan

luchtweerstand +rolweerstand op de caravan 2000 N. 
Bij constante snelheid (nettokracht = 0) is de trekkracht in de dissel 2000 N. 

MAAR dat wil niet zeggen dat de aandrijfkracht van de motor ook 2000 N is. De trekkende auto heeft zijn eigen lucht- en rolweerstand (bijv 1000 N) en dus zal de motorkracht 3000 N moeten bedragen. 

Stel massa caravan 800 kg,  massa auto 1600 kg. Ik trap op het as om te versnellen met 1,5 m/s² 

Daarvoor is nu een motorkracht nodig van F= ma = (800+1600) x 1,5 = 3600 N. Niet te vergeten natuurlijk de lucht- en rolweerstand, +3000 N geeft totaal 6600 N 

Om de caravan te versnellen moet de kracht in de dissel toenemen met F=ma = 800 x 1,5 = 1200 N Niet te vergeten natuurlijk de lucht- en rolweerstand, +2000 N geeft totaal 3200 N 

Om de auto te versnellen is een motorkracht nodig van F=ma = 1600 x 1,5 = 2400 N, Niet te vergeten natuurlijk de lucht- en rolweerstand, +1000 N geeft totaal 3400 N voor de auto

3200 + 3400 = uiteraard netjes de totale 6600 N. 

de winnende trekker komt ook in beweging en daar is ook kracht voor nodig. Zie rkenvoorbeeld auto met caravan hierboven

die elektromotor is vastgeschroefd, hoeft dus niet te versnellen , alles wat in beweging komt is de verliezende touwtrekker. 

Ik ben het met Jan eens dat dit een versie wordt van toestel van Atwood. Weliswaar gaat deze vraag over touwtrekkers die met hun hakken in de grond staan, maar voor het model en de vergelijkingen maakt het niet uit hoe die krachten veroorzaakt worden. De club die het hardste trekt versnelt achteruit, de andere club gaat over de lijn. Maar beide massa's hebben dezelfde grootte van versnelling.

Een AI zal hier voorlopig geen raad mee weten.

Dag allen,
Om (denk)fouten en misverstanden van mij en anderen te vermijden:
• zeg ik erbij of ik spreek over Lucas' vraag 1 óf vraag 2 óf iets anders, namelijk...
• zeg ik wie/wat een kracht uitoefent op wie/wat
• haal ik er liefst geen dingen bij waar Lucas' vragen geen informatie over bieden
• blijf ik zoveel mogelijk bij de vraag en maak ik de situatie niet onnodig ingewikkeld
Waar ik onvoldoende/onduidelijke/foute uitleg geef, hoor ik het graag.
Groet, Jaap

Dag Lucas,
Nu over vraag 1, niet vraag 2.
a. Ben je het eens met de conclusie dat de spankracht in het touw $100\,\text{N}$ is?
b. Ben je het ermee eens dat de vragen van Jan (01.11.2025 om 09.19 uur) leiden het antwoord 'de spankracht is $100\,\text{N}$'?
c. Ben je het ermee eens dat mijn aanpak (02.11.2025 om 23.35 uur) leidt tot hetzelfde antwoord 'de spankracht is $100\,\text{N}$'?
d. Zijn we klaar met vraag 1? Zo nee, wat moet er nog over vraag 1?
Straks meer over vraag 2.
Groet, Jaap

Jaap: Het is nodig om er dingen bij te halen waar de vraag geen informatie over verschaft: de (verhouding van) de massa's van beide touwtrekkers. Of een aanname te maken, dat beide mass's even groot zijn.

Oke, als ik jou goed begrijp Jan dan werkt het zo, weer een voorbeeldje:

Mijn hand weegt 1kg. Ik houd via een touw een gewicht beet van 1kg. Er is 10N nodig om het gewicht op zijn plek te houden tegen de zwaartekracht in. Nu oefent mijn hand een kracht uit van 20N naar boven. De versnelling is dus 10N/2kg = 5m/s², want er is ook kracht nodig om mijn hand te accelereren. Spanning in het touw wordt: 10N + 5m/s² x 1kg = 15N?

Maar wat nou als het gewicht van mijn hand niet gegeven is? Maar gewoon: het touw wordt met 20N naar boven getrokken? Dan moet de spanning in het touw toch gewoon gelijk zijn aan 20N? En het gewicht met 20N/1kg = 20m/s² versnellen?

Zo zie ik dit ook voor me bij de touwtrekkers: Als er alleen gegeven wordt: Aan de ene kant van het touw wordt met 800N getrokken en aan de andere kant met 1000N. Dan moet moet het touw toch sowieso een spankracht van 1000N voelen? 

Lucas: Ik interpreteer vraag 1 als dat de spanning in het touw gegeven is als 100 N. 

Voor vraag 2 werkt dat niet want dat wordt tegenstrijdig. Dus dan moet je dit zo interpreteren dat de ene touwtrekker zich afzet tegen de grond met 1000 N en de andere met 900 N. Óf de massa van het touw moet gegeven zijn. 

 Jaap  op 03 november 2025 om 11:32
Dag Lucas,
Nu over vraag 1, niet vraag 2.
a. Ben je het eens met de conclusie dat de spankracht in het touw 100N
is?
b. Ben je het ermee eens dat de vragen van Jan (01.11.2025 om 09.19 uur) leiden het antwoord 'de spankracht is 100N'?
c. Ben je het ermee eens dat mijn aanpak (02.11.2025 om 23.35 uur) leidt tot hetzelfde antwoord 'de spankracht is 100N'?
d. Zijn we klaar met vraag 1? Zo nee, wat moet er nog over vraag 1?
Straks meer over vraag 2.
Groet, Jaap

A, eens
B, eens
C, eens
D, ja; de totale kracht die nodig is om het gewicht te accelereren moet gewoon doorgegeven worden via het touw. Ik moet er verder niet te moeilijk overna denken. Zwaartekrachtversnelling + versnelling naar boven maal massa is kracht. Dus ja, 100N.

Maar zo zie ik dit nu dus ook voor me bij vraag 2. Ik heb in eerste instantie geen gewichten opgegeven bij de touwtrekkers. Gewoon: aan één kant wordt met 1000N getrokken en aan de andere kant met 900N. Zou ik een weegschaal in het touw plaatsen dan moet deze volgens mij gewoon 100kg (of 1000N) aangeven. Netto 100N naar één kant, gedeelt door het gewicht van de touwtrekker van 900N zou dan de versnelling moeten geven (Wat onmogelijk snel is natuurlijk). Maar hoe ik het zie blijft de spanning in het touw 1000N.

dan bedenken we dat je nu aan beide kanten met 900 N MINDER gaat trekken. aan één kant niksnulnada, aan de andere kant 100 N. 
Als ik dat op video zet en naar dat touwtje kijk, wat zie ik dan? 

Als je moeite hebt je dat voor te stellen bedenk dan een elastiek ipv een touw.
Aan de ene kant trek je met 100 N, aan de andere kant trek je niet.
Hoe ver rekt dat elastiek uit?
Conclusie spankracht in elastiek? 

dan bedenken we dat je nu aan beide kanten met 900 N MINDER gaat trekken. aan één kant niksnulnada, aan de andere kant 100 N. 
Als ik dat op video zet en naar dat touwtje kijk, wat zie ik dan? 

Als je moeite hebt je dat voor te stellen bedenk dan een elastiek ipv een touw.
Aan de ene kant trek je met 100 N, aan de andere kant trek je niet.
Hoe ver rekt dat elastiek uit?
Conclusie spankracht in elastiek? 


Goed punt.
Als het touw zelf geen massa heeft dan heeft hij inderdaad geen spankracht, maar accelereert wel oneindig snel met een kracht van 100N. Dus jij zegt, met alleen de gegevens 1000N naar links en 900N naar rechts ervaart het touw een spankracht van 900N?

Dan is het vicieuze cirkeltje in mijn hoofd weer rond, want waarom is dit anders bij het gewicht aan het touwtje? 100N naar boven zonder gewicht is oneindige acceleratie. 100N naar boven met 10N aan gewicht moet dus ook maar 10N aan spankracht in het touw zijn?

Lucas: 100 N spankracht naar boven met 10 N gewicht (dus 1 kg massa) geeft een versnelling a = Fₜ/m = 90/1 = 90 m/s². Zoals gewoonlijk wordt de massa van het touw verwaarloosd. Dat betekent dan ook dat de spanning van het touw overal gelijk moet zijn. Anders heb je een tegenspraak geconstrueerd.

nee, want een blokje van 1 kg zal een zwaartekracht tegen de trekrichting in ondervinden van 10 N 
Maar zodra dat omhoog moet moet dat gaan versnellen en daarvoor is een kracht BOVENOP die zwaartekracht nodig. 
In dit geval zal de nettokracht 100-10= 90 N zijn dus versnelling a=F/m = 90/1 = 90 m/s² .

Dan is de spankracht dus de volle 100 N. ALS het trekkende object tenminste niet óók een massa heeft en niet óók zal gaan versnellen. 

Ik denk dat het lampje nu bij mij begint te branden.

Het is onmogelijk om in beide situaties de spankracht te bepalen met alleen de krachten.
Want bij 900N naar links van persoon A en 1000N naar rechts van persoon B weet je alleen dat de spankracht minimaal 900N moet zijn. Hoeveel spankracht er extra bij komt is afhankelijk van het gewicht van persoon B (als we ervan uitgaan dan persoon A 1000N blijft trekken wat zijn eigen gewicht ook is).

En bij het touwtje met 10N naar beneden en 100N omhoog precies hetzelfde. De spankracht moet minimaal 10N zijn, maar omdat we weten dat het gewicht 1kg is, komt daar 90N x 1kg bij. Dus 100N.

En als je 2 elektromotoren met elkaar laat touwtrekken, motor A trekt met 1000N en motor B trekt met 900N, dan is de spankracht in het touw dus minimaal 900N. Hoe je het totaal moet berekenen snap ik in deze situatie even niet omdat er geen gewicht is.

Dus als persoon A 1000N trekt ongeacht zijn eigen gewicht, en persoon B trekt met 900N en weegt 100kg, dan is er een netto kracht van 900N + 1m/s² x 100kg = 1000N.
Maar persoon A heeft zelf ook gewicht dus in werkelijkheid ligt het tussen de 900N en 1000N.

Probeer ook om niet in de war te raken een strak onderscheid te maken tussen gewicht en massa. En die massa is belangrijk zodra het object in beweging zal komen. Als persoon A kan gaan bewegen en persoon B niet (stel die kan gewoon blijven straan en dat touw inhalen) dan wordt de spankracht die 1000 N. 

En als de massa 4 kg zou zijn is er een gewicht van 40 N dat tegen de beweging in werkt, en dan resteert er een nettokracht van 60 N en wordt de versnelling a=F/m = 60/4 = 15 m/s². ALS het trekkende object tenminste niet óók een massa heeft en niet óók zal gaan versnellen. (zie gevalletje auto plus caravan) 

als beide motoren niet van hun plaats kunnen zal in theorie ( touw en  as/motor met verwaarloosbare massa) dat touw met een enorme versnelling naar motor A schieten 
a= F/m = 100/0,000 000 000 .....  = heel veel. 

in werkelijkheid gaat het stuk touw tussen beide motoren lineair versnellen, de stukken die rond de assen zitten moeten rotationeel versnellen, de in het echt niet massaloze assen en rotoren van de elektromotoren  moeten rotationeel gaan versnellen, en allerlei inductie-effecten van de versnellende rotatie in het systeem rotor-stator hebben ook nog zo hun eigen krachteffecten. De spankracht zal dus op een lastig te bepalen grootte tussen 900 en 1000 N terecht komen

Lucas: "Hoe je het totaal moet berekenen snap ik in deze situatie even niet omdat er geen gewicht is."

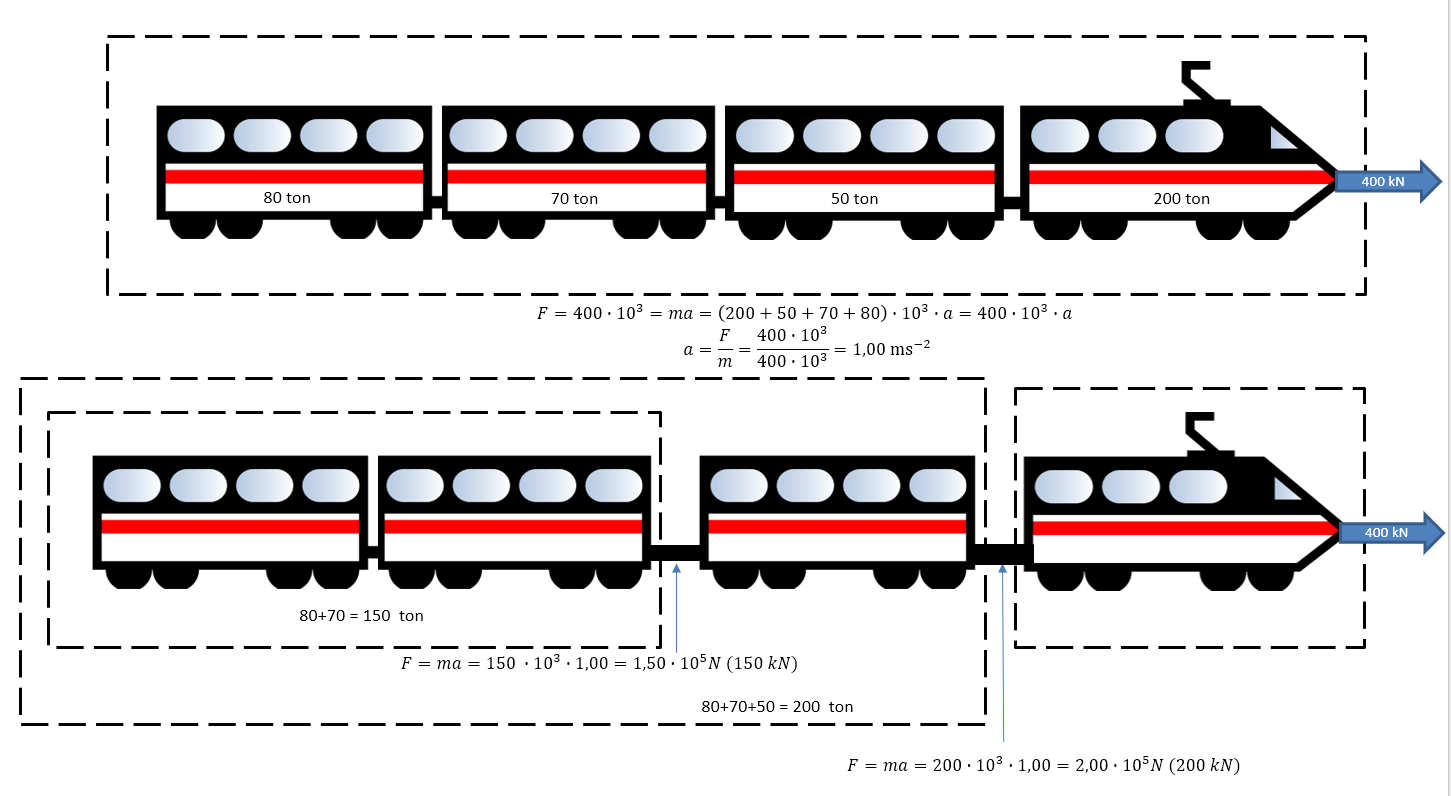
Er is altijd wel gewicht: een dik touw, of een zware ketting, of een rij treinwagons. Als daaraan getrokken wordt met verschillende krachten links en rechts, versnelt die als geheel, maar de spanning hangt af van de plaats. Beschouw bijvoorbeeld het geval van een aantal wagons.

Bedankt mannen. Ik denk dat het me helemaal duidelijk is. 

In aanvulling op Pieters reactie over spanning tussen wagonnen, gebruikte ik vaak onderstaande tekening. De hele trein gaat met a = 1 m/s² maar de spanning tussen wagonnen hangt af van hoeveel wagonnen (en hun massa) moesten worden getrokken door het voorste deel van de trein.

Dag Lucas,
Dank voor je reactie van 03.11.2025 om 12.03 uur over vraag 1.
We zijn klaar met vraag 1, als anderen het er ook mee eens zijn.
Wat in vraag 1 'het gewicht' heet, noem ik verder 'het blok' om misverstand te vermijden.

Je schrijft op 03.11.2025 om 09.24 uur:
'Jij zegt, spankracht in mijn laatste voorbeeld blijft 900N. Jaap en Jan lijken te zeggen dat de spankracht gelijk is aan de krachtwaarmee getrokken wordt. En nu weet ik het niet meer :)'

De spankracht van $900\,\text{N}$ die Theo (03.11.2025 om 09.15 uur) en ik (02.11.2025 om 23.49 uur) noemen, gaan over jouw vraag 2.
Je uitspraak 'Jaap en Jan lijken te zeggen dat de spankracht gelijk is aan de krachtwaarmee getrokken wordt' gaat over vraag 1.

Jan schrijft op 01.11.2025 om 09.19 uur:
'2) is een zelfde gevalletje als 1). kantel de hele situatie 90 graden, bedenk een persoon met een gewicht van 900 N die hangend aan een touw met een kracht van 1000 N omhoog wordt getrokken.'
MIsschien komt je opmerking 'En nu weet ik het niet meer' doordat je aanneemt dat vraag 2 net zo gaat als vraag 1, terwijl je hier verschillende conclusies leest over de grootte van de spankracht.

Bij vraag 1 en 2 zijn een paar dingen 'een zelfde gevalletje': er is een touw; op beide uiteinden wordt een trekkende kracht uitgeoefend; gevraagd wordt de spankracht; …
Maar om te beredeneren hoe groot de spankracht is, is vraag 2 niet 'een zelfde gevalletje' als vraag 1. We kunnen bij vraag 2 niet dezelfde methode volgen als bij vraag 1. We kunnen bij vraag 2 niet op dezelfde manier een conclusie over de spankracht trekken als bij vraag 1. Wat is bij vraag 2 anders dan bij vraag 1?

Eerst vraag 1.
Zoals je op 03.11.2025 om 12.03 uur over vraag 1 correct zegt, oefent het touw een kracht op het blok uit:
• om het blok te accelereren (dat vergt $M\cdot a=1\cdot 90=90\,\text{N}$) en
• om de zwaartekracht op het blok te compenseren (dat vergt $10\,\text{N}$).
Deze kracht van $90+10=100\,\text{N}$ van het touw op het blok heet de spankracht. We weten dat het $100\,\text{N}$ is, want we hebben het netjes beredeneerd (Jan) of berekend (Jaap).
Uit vraag 1 weten we de $100\,\text{N}$ waarmee de persoon aan 'touw plus blok' trekt en de $10\,\text{N}$ zwaartekracht waarmee de aarde aan 'touw plus blok' trekt. Via de versnelling van het blok krijgen we de spankracht van $100\,\text{N}$ en dat is een interne kracht binnen het geheel van 'touw plus blok'.

Nu vraag 2, waarin we lezen 'De ene persoon [zeg Jip] trekt met 900N aan het touw en de andere [zeg Janneke] met 1000N aan het touw.'
Volgens de derde wet van Newton trekt het touw omgekeerd ook met $900\,\text{N}$ aan Jip. Deze kracht heet de spankracht. We weten dat het $900\,\text{N}$ is, want dat volgt uit de informatie van vraag 2.
Jip trekt met $900\,\text{N}$ van Jip aan het touw. Janneke trekt ook met $900\,\text{N}$ aan het touw (zie verder). Deze twee krachten zijn even groot, tegengesteld gericht langs dezelfde werklijn en ze werken op hetzelfde ding (touw), dus deze twee krachten heffen elkaar op. Ze veroorzaken geen versnelling van het touw. Het zijn deze twee krachten, op het touw uitgeoefend door Jip en Janneke, elk $900\,\text{N}$, die de spankracht oproepen.

Dus wat is bij vraag 2 anders dan bij vraag 1?
Uit vraag 2 weten we de $1000\,\text{N}$ en $900\,\text{N}$ waarmee Jip en Janneke aan het touw trekken. Uit de derde wet van Newton volgt de spankracht van $900\,\text{N}$. Bij vraag 2 is de spankracht een kracht op de buitenwereld die bestaat uit Jip en Janneke. Bij vraag 1 was de spankracht een interne kracht op een onderdeel van 'touw plus blok' waar de bekende krachten op werken.

Jazeker, Janneke trekt bovendien nog met $1000-900=100\,\text{N}$ aan het touw.
De resulterende kracht van $100\,\text{N}$ is een kracht op het touw en wat deze kracht doet, is aan het touw een versnelling geven volgens $F_\text{res}=m_\text{touw}\cdot a$. De $F_\text{res}=100\,\text{N}$ roept geen spankracht op.

Logisch, toch? Als Jip blijft trekken met $900\,\text{N}$ en Janneke met $1000\,\text{N}$ en we vervangen het touw herhaaldelijk door een zwakker touw, dan breekt het door de twee maal $900\,\text{N}$ die Jip en Janneke op het touw uitoefenen. Het breekt niet doordat een resulterende kracht van $100\,\text{N}$ aan het touw een versnelling geeft.
Het oorspronkelijke touw is belastbaar met $900\,\text{N}$ tegen $1000\,\text{N}$. Het breekt ook niet als Jip trekt met $0,001\,\text{N}$ in plaats van $900\,\text{N}$ en Janneke met $100,001\,\text{N}$ in plaats van $1000\,\text{N}$ zodat wel $F_\text{res op touw}=100\,\text{N}$.

We lezen in vraag 2 verder niets over deze personen of waar de wedstrijd plaatsvindt. Misschien is de massa van Jip $50\,\text{kg}$ en die van Janneke $150\,\text{kg}$ of omgekeerd. Misschien zijn Jip en/of Janneke vastgelijmd op de grond of zweven ze gewichtloos in een ruimtesonde ver van alle hemellichamen. Dat weten we niet en het maakt ook niet uit voor de grootte van de spankracht, die $900\,\text{N}$ bedraagt.
Groet, Jaap

En dankzij dit topic snap ik het toestel van Atwood ook denk ik: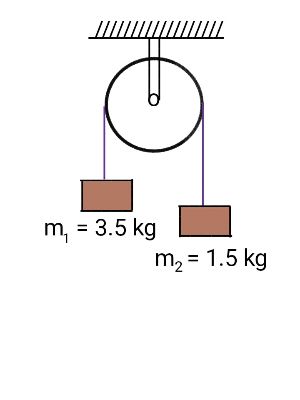

Er is een netto kracht van 20N in dit voorbeeld. De versnelling is dus 20N / 5kg = 4m/s². De spankracht in het touw moet dan 4m/s² x 1,5kg + 15N = 21N zijn?

dag Jaap, 
wel zo lang Jip dat touw blijft vasthouden want dan zal Jip gaan versnellen. Zie gevalletje auto en caravan. 

Groet, Jan

yep, en kun je die 21 N ook terugvinden in dat touwdeel boven dat blok van 3,5 kg? Want als touw en katrolwiel massaloos zijn moet ook dáár 21 N aanwezig zijn

Lucas: Bij dit toestel van Atwood is de versnelling inderdaad 4 m/s². Test je berekening ook op de andere massa. De totale kracht daarop is 4*3,5 = 14 N naar beneden. De zwaartekracht is 35 N, de spanning trekt met 21 N opwaarts. Dus dat klopt precies!

We lezen in vraag 2 verder niets over deze personen of waar de wedstrijd plaatsvindt. Misschien is de massa van Jip  en die van Janneke  of omgekeerd. Misschien zijn Jip en/of Janneke vastgelijmd op de grond of zweven ze gewichtloos in een ruimtesonde ver van alle hemellichamen. Dat weten we niet en het maakt ook niet uit voor de grootte van de spankracht, die  bedraagt.
Groet, Jaap


Ik kan je formules helaas niet mee kopiëren en plakken. Maar als geen massa van beide bekend is, en Jip trekt aan Janneke met 1000N en Janneke trekt met 900N terug, dan zou de spankracht toch eigenlijk 1000N moeten zijn? Want hoe zwaar of licht Janneke ook is, blijkbaar is Jip in staat om Janneke te versnellen met een kracht van 1000N?

yep, en kun je die 21 N ook terugvinden in dat touwdeel boven dat blok van 3,5 kg? Want als touw en katrolwiel massaloos zijn moet ook dáár 21 N aanwezig zijn

(10m/s² - 4m/s²) x 3,5kg = 21N

test 

in een quote wordt LaTeX naar gewoon ascii vertaald, in elk geval voor eenvoudige LaTeX als dit.
Maar de quotefunctie is, voor gewone gebruikers, uitgeschakeld. 
Copypasten van de LaTeX in Jaaps bericht werkt inderdaad niet. 

Ik ga dat eens melden want echt handig is dat niet. 

Groet, Jan

Dag Lucas,
Je schreef: 'Maar als geen massa van beide bekend is, en Jip trekt aan Janneke met 1000N en Janneke trekt met 900N terug, dan zou de spankracht toch eigenlijk 1000N moeten zijn? Want hoe zwaar of licht Janneke ook is, blijkbaar is Jip in staat om Janneke te versnellen met een kracht van 1000N?'

Vraag 2 is niet zoals je schrijft. De eerste persoon (in mijn tekst Jip) trekt volgens vraag 2 met $900\,\text{N}$ aan het touw. De tweede persoon (mijn Janneke) trekt met $1000\,\text{N}$ aan het touw. Door de resulterende $100\,\text{N}$ krijgt het touw een versnelling.

Of een persoon door de kracht van de ander een versnelling ktijgt, weten we uit vraag 2 niet. Dat hoeven we ook niet te weten om met de informatie uit vraag 2 vast te stellen dat de spankracht $900\,\text{N}$ is. Dat is mijn antwoord van 03.11.2025 om 23.49 uur op je oorspronkelijke vraag 2.
Groet, Jaap

Dag Pieter,
Je schrijft op 03.11.2025 om 18.50 uur: 'Perplexity heeft het gewoon fout (gisteren om 15:06)'. Ik heb nog niet gelezen waarom het antwoord van Perplexety op vraag 2 dan fout zou zijn. Kun je uitleggen waarom Perplexety het fout heeft, als we net als Perplexety uitgaan van wat in vraag 2 staat?

Je schrijft ook 'En jij hebt het ook niet goed, want met alleen kracht kom je er niet.' Op 02.11.2025 om 23.49 uur heb ik de spankracht berekend zonder aanname over de massa of versnelling van de personen, zonder iets erbij te interpreteren. Wat heb ik om 23.49 uur dan niet goed gedaan, als we afgaan op hetgeen in vraag 2 staat?

Zoals je zegt, ook vraag 2 is een goede vraag van Lucas. Mijns inziens heb ik om 23.49 uur een goed antwoord gegeven.
Groet, Jaap

Dag Jan,
Op 03.11.2025 om 15.18 uur schrijf je:
'wel zo lang Jip dat touw blijft vasthouden want dan zal Jip gaan versnellen'
als reactie op mijn uitspraak van 14.52 uur
'De $F_\text{res}=100\,\text{N}$ roept geen spankracht op.'

We weten niet of Jip met het touw in de hand zal versnellen. Er zijn andere mogelijkheden. Misschien blijven Jip en Janneke op hun plek, vastgelijmd aan de grond, en laat Jip het touw door zijn handen slippen en terwijl hij er met $900\,\text{N}$ aan blijft trekken? Misschien haalt Janneke het touw steeds sneller in, terwijl zij er met $1000\,\text{N}$ aan blijft trekken?

Omdat we dit niet weten, doe ik er geen veronderstelling over en blijf ik bij hetgeen in vraag 2 staat. De resulterende $100\,\text{N}$ veroorzaakt een versnelling van het touw. Dat volgt rechtstreeks uit de gegevens. Of de resulterende kracht ook gepaard gaat met een versnelling van een of beide personen, is onbekend en daarom speculeer ik er niet over.
We hoeven geen versnelling of massa van de personen te weten om Lucas' vraag 2 te beantwoorden: zie 02.11.2025 om 23.49 uur.

Dat de resulterende $100\,\text{N}$ met de gegevens uit vraag 2 niet bepalend is voor de spankracht, heb ik al beargumenteerd in de alinea 'Het oorspronkelijke touw is belastbaar...'  Omgekeerd: het touw breekt als Jip te hard trekt, zeg met $900\,\text{teranewton}$ in plaats van $1000\,\text{N}$ terwijl Janneke trekt met met $0,001\,\text{newton}$ meer dan Jip. Het touw breekt dan door de $900\,\text{teranewton}$ waarmee ieder trekt, niet door de geringe resulterende extra kracht die Janneke uitoefent. Ik haal er niets nieuws bij, varieer alleen met de gegevens.
Groet, Jaap

Klopt. De principes van krachten en versnellingen in dit soort gevallen heb je dus intussen begrepen. De rest is een kwestie van interpreteren welke krachten er in en rond het systeem spelen, en dat dat niet altijd eenvoudig is blijkt wel uit bovenstaande discussie. 

Groet, Jan

@Jaap

Dus jij zegt eigenlijk: Als er geen massa opgegeven is dan ga je ervan uit dat er geen massa is en het touw met een nettokracht van 100N dus oneindig versnelt?

Daar zit de "idealisatie" van het probleem-oplossen. Bijna altijd wordt het touw als massaloos beschouwd (wat niet waar is - neem een scheepskabel, die is echt niet massaloos).

Maar ALS je dat aanneemt, en weet dat F = ma dan is a = F/m = F/0 = onbepaald (natuurkundig meestal vervang je dan 0 door iets heel kleins, 0,000....000 001) waardoor de kracht heel groot (zeg maar "oneindig") wordt. Wat natuurlijk in werkelijkheid ook niet waar is (al was het maar omdat je klassiek dan boven de lichtsnelheid komt in een fractie (ook 0) van een seconde).

Theo: "waardoor de kracht heel groot "

Je bedoelde "waardoor de versnelling oneindig wordt".

Dan glijdt Jip en Janneke natuurlijk dat touw door hun handen, en die hebben dan niets meer met het touw te maken, dus dat is ook daarom niet zo'n zinnige interpretatie van de geschetste situatie.

Dag Lucas,
Dat het touw door een nettokracht van $100\,\text{N}$ een oneindige versnelling krijgt, heb ik niet gezegd.
Op 02.11.2025 om 23.49 uur schrijf ik over vraag 2 dat de versnelling van het touw $a=F_\text{res}/m=100/0$ wiskundig onbepaald is ('we weten het niet, geen getal') en dat het natuurkundig onmogelijk is. Daarom schreef ik: 'Het touw kan niet massaloos zijn.' Tja, wat nu?
Op 03.11.2025 om 11.31 uur schrijf ik:
'• blijf ik zoveel mogelijk bij de vraag en maak ik de situatie niet onnodig ingewikkeld'.
Een 'oneindige versnelling' lukt niet, dus kan ik vraag 2 niet exact nemen. Ik blijf zoveel mogelijk bij de vraag, maar kan alleen een antwoord geven als ik aan het touw enige massa toeken.

De situatie met het toestel van Atwood is leerzaam, maar wel anders dan vraag 2.
• Wat bij Atwood aan het touw trekt, zijn de twee blokken. Wat een versnelling krijgt, zijn de blokken $m_1$ en $m_2$ (en voor de liefhebbers ook het koord en de katrol). Op dit versnelde geheel werkt een kracht van buitenaf, namelijk de zwaartekracht waarmee de aarde aan de blokken trekt. Plus, zo je wilt, wat luchtweerstand enzovoort. De spankracht is hier een interne kracht binnen het versnelde geheel: het is een kracht van het koord op de twee blokken.
• Dat is anders in vraag 2, waar het Jip en Janneke zijn die een kracht op het touw uitoefenen. Wat een versnelling krijgt, is in elk geval het touw. De spankracht is hier een kracht van het versnelde geheel (=het touw) op de buitenwereld (=Jip en Janneke). Anders dan bij Atwood is de gevraagde spankracht in vraag 2 geen interne kracht.

Natuurlijk kunnen we aan Jip en Janneke een massa toekennen en iets zeggen over eventuele krachten die van buitenaf op Jip en Janneke werken. Bij voorbeeld schuifwrijvingskracht van de grond op hun voeten. Ook in zo'n situatie kun je de spankracht berekenen. Dit lijkt meer op 'Atwood'. Maar het is wel een andere vraagstelling dan jouw vraag 2.
Groet, Jaap

Ik vind hoe Jan het uitgelegd heeft met het Atwood systeem het meest logisch klinken, dus dat ga ik onthouden. 

Jaap, ik snap niet helemaal wat je probeert uit te leggen. En met "jij zegt dus eigenlijk" bedoel ik natuurlijk niet dat je dat letterlijk zegt, maar meer hoe ik zelf het plaatje kloppend kan maken in mijn hoofd.

Ik begreep mijn denkfout uiteindelijk, juist omdat ik geen massa in mijn verhaal had verwerkt. Maar als er geen massa is, en er wordt met een nettokracht van 100N aan het touw getrokken, dan moet het touw dus wel oneindig versnellen??

Dag Lucas,
Zoals je wilt, onthoud 'Atwood'. Dat is dan vraag 3.

Ik ben vooral ingegaan op vraag 2.
Als het touw geen massa heeft en er werkt een resulterende kracht van $100\,\text{N}$ op, dan kan ik alleen zeggen dat de versnelling 'onbepaald' is.
Op de wiskundige manier kunnen we spreken van een 'limiet'. Als $F_\text{res}=100\,\text{N}$ en deze kracht werkt op een steeds kleiner gekozen massa, dan 'is de limiet van $a$ oneindig', 'gaat de versnelling naar oneindig'. Dat is een wiskundige uitspraak, want natuurkundig en praktisch kan de versnelling niet oneindig zijn. Daarom heb ik niet gezegd dat het touw een oneindige versnelling krijgt.
Groet, Jaap