Dit ziet er ongeveer zo uit als bij een wijnglas denk ik, zie de gelinkte video. En die 1,10 meter, is dat de lengte van de omtrek van de rand van die klok?

https://www.youtube.com/shorts/ZdWlAr_ARuM 

beste Pieter bedankt voor u reactie de omtrek moet je nog berekenen aan de hand van omtrek diameter keer pi 

Terzijde, vermoedelijk wordt in deze wat verminkte vraag deze klok bedoeld:
https://www.netherlandsandyou.nl/web/united-states/about-us/carillon

Hier een opname van het moment waarop de Marshallklok op zijn plaats wordt gehesen: 
https://youtu.be/lQrJDl3s5Kk?t=160

Moderator

Dag Isa,

Opgave 12
Er staat: 'De meting begint op een punt dat samenvalt met een buik van de grondtoon.'
Kun je wat dit betreft nog iets verbeteren aan je schets?
Wat zet je bij de horizontale as en bij de verticale as?

Opgave 13
We weten al: 'Bij de grondtoon bestaat deze uit twee hele golven. De frequentie is 162 Hz.'
Een hele golf: dat is twee buiken en twee knopen op de hele cirkelrand.
We weten ook: 'de frequentie van de eerste boventoon is 243 Hz'.
De frequentie van de eerste boventoon is 3/2 maal zo groot als die van de grondtoon.
Hoeveel golven heb je dan op de cirkelrand van de klok?
Vind je de onderstaande tekening goed of fout voor opgave 13? Waarom?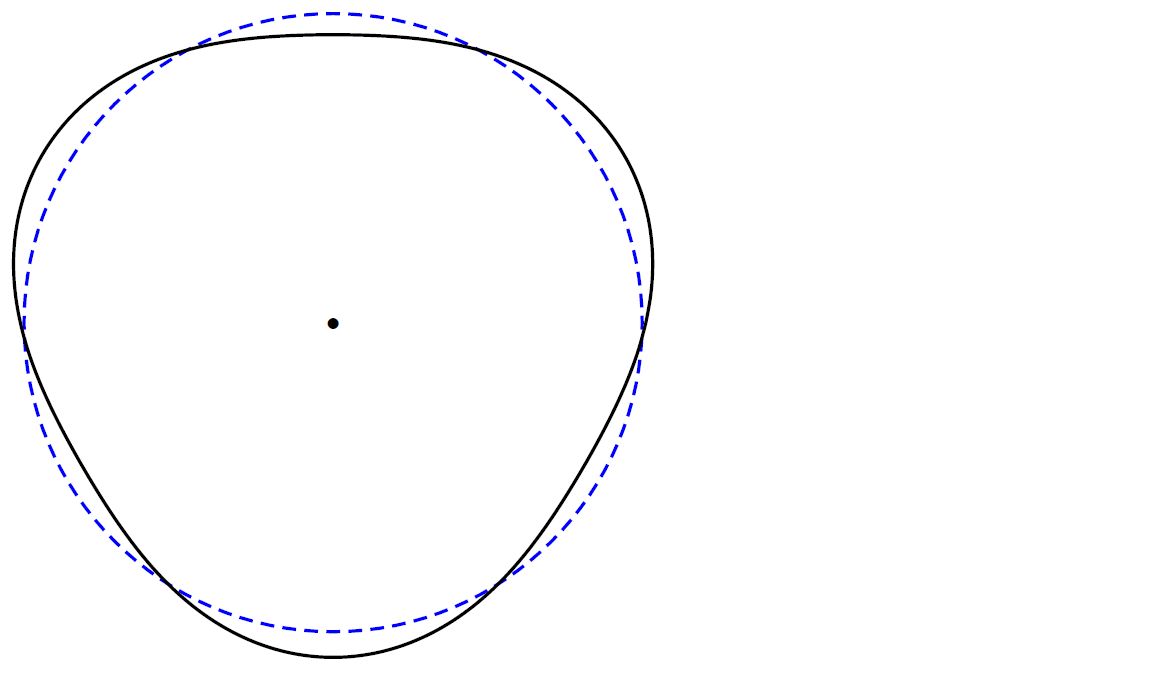

Groet, Jaap

Ook det terzijde: ik vraag me af of het allemaal wel klopt in de opgave. De nieuwe Marshall klok is de bourdon, de grote klok van het carillon, 1,75 meter diameter, toonhoogte B♭0 volgens Wikipedia en dat is 29 hertz.

De reden waarom ik dit ging opzoeken is dat luidklokken etc in het algemeen geen harmonische spectra hebben. Het lijkt me uiterst onwaarschijnlijk dat de eerste boventoon op 3/2 van de frekwentie van de grondtoon ligt. Ik heb zelf een klein klokje en daar zijn de frekwenties 1370 Hz en 3780 Hz.

Dag Pieter,
Inderdaad kan men zich afvragen of de informatie in de opgave geheel juist is.
Er staat: 'Je kunt de onderrand van de klok beschouwen als een snaar in de ronde waarbij de uiteinden met elkaar verbonden zijn. Bij de grondtoon bestaat deze uit twee hele golven. De frequentie is 162 Hz. [$\ldots$] de frequentie van de eerste boventoon is 243 Hz.'
De verhouding van de frequenties van grondtoon en eerste boventoon is 2:3.
Maar bij een snaar met twee vaste uiteinden is de verhouding van de frequenties bij de grondtoon en de opeenvolgende boventonen 1:2:3:...
Dit doet vermoeden dat 162 Hz de eerste boventoon zou kunnen zijn en 243 Hz de tweede boventoon.
Zichtbaar trilt het wijnglas in de film met twee hele golven op de omtrek. Is er een natuurkundige oorzaak waardoor dat niet een enkele hele golf op de omtrek zou kunnen zijn? Ook Niels Bohr ging er, voordat de quantummechanica werd uitgevonden, vanuit dat bij een waterstofatoom in de grondtoestand een enkele De Brogliegolflengte van het elektron past op de omtrek van de 'baan' van het elektron om de kern.

Over dit alle hoeft Isa zich geen zorgen te maken.
Groet, Jaap

Dag Jaap

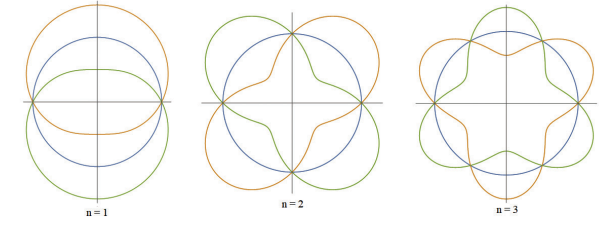
De mode met één golflengte op zo'n ring valt wel te tekenen, maar je ziet in die figuur met n = 1 dat het zwaartepunt dan ook heen en weer beweegt. Misschien dat die beweging snel gedempt wordt, of nauwelijks door een klepel wordt aangeslagen? Zoiets als bij de stemvork waar ook de tanden naar elkaar toe òf van elkaar af bewegen.

Ja, er is een analogie met het Bohr-model, zoals in deze demonstratie met een trillende cirkelvormige snaar waar de knopen en de buiken goed zichtbaar zijn. Anders dan bij een gitaar is de terugdrijvende kracht niet de mechanische spanning maar de stijfheid van de snaar en daaardoor is de golflengte niet omgekeerd evenredig met de frekwentie.
 
  
Een luidklok is nog een stuk ingewikkelder, want die heeft ook boventonen die in de andere richting trillen.

Om weer terug te komen op de opgave over de geluidsterkte: de geluidssterkte is altijd positief. En het sterkst bij de buiken.

Er zijn inderdaad vier buiken bij een meting rond de luidklok, dus vier maxima van 0 tot 360°, maar  het patroon moest volgens de opgave beginnen bij een buik.