Newton op de noordpool
noah stelde deze vraag op 06 maart 2023 om 13:26.Hallo mensen
Newton deed een experiment in gedachten. Van een berg op de noordpool gooi je een steen weg. Als je harder gooit komt de steen verder op de grond. Dat zie je in de tekening.
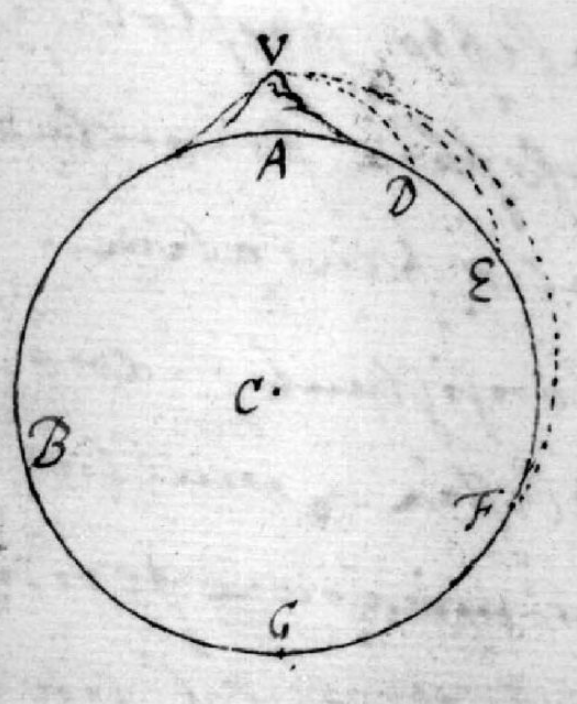
In plaats van de berg maken we een toren op de noordpool. De hoogte van de toren is de helft van de straal van de aarde.
Neem aan dat de aarde een bol is met overal gelijke samenstelling en dat de aarde op een vaste plaats blijft en niet om zijn as draait. Hou geen rekening met de maan, zon en zovoort. Luchtwrijving verwaarlozen.
Bereken de snelheid waarmee je de steen van de toren moet gooien zodat hij over E en F heen in G op de zuidpool landt.
okay, wet van energiebehoud 0.5*m*v1^2-GM*m/1.5R=0.5m*v2^2-GMm/R en R is de straal van de aarde
Je kan m en R wegstrepen 0.5*v1^2-GM/1.5=0.5*0^2-GM/1 dus 0.5v1^2=GM/1.5-GM/1 maar als je dat invult krijg je een mingetal
Hoe moet je dit doen?
Reacties
Het gaat hier echter om krachten: de aarde trekt met GMm/(R+h)2 (als h = hoogte vanaf de aardbol) en om in een cirkelbaan te blijven (en dus wel continu te vallen maar nooit op de grond te komen omdat het aardoppervlak net zo snel meebuigt) is een kracht mv2/(R+h) nodig.
Die kracht wordt door de aantrekkingskracht geleverd. Maw
algemene kracht nodig om te draaien = mv2/(R+h)
wie levert die algemene kracht? De zwaartekracht (in andere gevallen van cyclotron: Lorentzkracht)
Hoe groot is de zwaartekracht? GMm/(R+h)2
Ofwel
mv2/(R+h) = GMm/(R+h)2
nou zie ik hoe ik een mingetal kreeg. ik heb ingevuld v2=0 maar dat is als de steen op de zuidpool ligt. je moet v2 laten staan die weet je niet
en ik heb R weg gestreept maar dar kan niet want in 0.5m*v^2 zit geen r
dus het is 0.5*v1^2=0.5v2^2+GM/1.5R-GM/R Ris straal van aarde
niet fijn want v1 en v2 weet je allebei niet dus hoe kan je v1 berekenen?
dankjewel voor de hulp
1/2 mv2 is de kinetische energie van een ronddraaiend voorwerp (zoals aardbol) , Ezw = - GMm/r is de zwaarte-energie die het voorwerp met masssa m heeft in het zwaartekracht veld van de grote massa M (bijv. de zon) op afstand van baanstraal r (niet de bol-straal van zon of aarde).
1/2 mv2 = GMm/r stelt dat de kinetische energie gelijk zou zijn aan de zwaarte-energie. Waarom zou dat moeten? Nogmaals voor het ronddraaien van een massa om een veel grotere massa beschouw je krachten, geen energieen.
Noah begint goed met de wet van energiebehoud
Ek1+Eg1=Ek2+Eg2
1/2*m*v1^2-G*M*m/r1=1/2*m*v2^2-G*M*m/r2
r1=1.5*R want de toren is 1/2*R hoog R is de straal van de Aarde
r2=R want de steen komt op de Aarde
Deel door m de massa van de steen 1/2*v1^2-G*M/[1.5*R]=1/2*v2^2-G*M/R
dus Noah deed 1/2*v1^2=1/2*v2^2+G*M/[1.5*R]-G*M/R dat is ok.
Voor G en Maarde en Raarde heb je BiNaS maar behalve v1 weet je v2 ook niet. Je kunt v1 uitrekenen als je nog een andere relatie tussen v1 en v2 hebt.
De steen maakt geen halve cirkel maar een halve ellips want het startpunt is verder van het centrum van de Aarde (brandpunt Kepler) dan het eindpunt na een halve omloop. De steen begint in het apogeum en eindigt in het perigeum als het ware. Daar is de r-vector verticaal en de v-vector horizontaal dus voor het baanimpulsmoment geldt L/msteen=r*v
In het startpunt is dat L/m=r*v=1.5*R*v1 en in het eindpunt R*v2
Impulsmoment is constant in dit experiment dus R*v2=1.5*R*v1 en v2=1.5*v1
Zet dit in de formule van energiebehoud 1/2*v1^2=1/2*[1.5*v1]^2+G*M/[1.5*R]-G*M/R
en je vindt v1^2=8/15*G*M/R en v1=5776 m/s ongeveer.
Meneer De Klerk zegt
1/2 mv2 = GMm/r stelt dat de kinetische energie gelijk zou zijn aan de zwaarte-energie. Waarom zou dat moeten?
Hoezo? Noah zegt niet 1/2 mv2 = GMm/r
Meneer De Klerk zegt
De vallende steen heeft met energie niets te maken: het zijn krachten die zorgen dat iets in een cirkelbaan ronddraait
Vreemd. Dit is geen cirkelbaan. De snelheid verandert qua grootte (en richting) dus Ek en Eg veranderen. Hoezo heeft het niets met energie te maken? Een kracht die arbeid verricht en verandering van energie zijn twee kanten van dezelfde medaille.
Meneer De Klerk zegt
Nogmaals voor het ronddraaien van een massa om een veel grotere massa beschouw je krachten, geen energieen.
De startsnelheid is berekend met energie en impulsmoment. Als meneer De Klerk liever werkt met kracht maak dan een model en v1=sqrt(8/15*G*M/R) startsnelheid. De steen komt op de Aarde na een halve ellips.
Ibtihal
natuurkundedocent van Noah
