De potentiele energie (tov laagste punt) kun je misschien beredeneren a.d.h.v. onderstaande tekening.

Bedankt!
Het probleem is dat ik in mijn eigen uitwerking geen fouten opmerk. Ik had graag geweten wat ik fout heb gemaakt.

om te beginnen gebruik je een formule voor de uitwijking van een massa die trilt aan een veer, in plaats van een slinger

Een slinger heeft geen veerconstante, formules met veerconstantes kun je dan ook lastig gebruiken voor een slinger. 

Hallo Theo

met jouw tekening doe ik h=1cm*tan alfa

T=3s en T=2pi*wortel L/g dus L=2.24m

sin alfa=0.01/L dus alfa=0.00447rad

h=1cm*tan alfa=0.00447cm

Epot=5*9.81*0.0000447=0.0022J

Bedoel je dat? maar dat is niet 0.0011J van het antwoordboek

Daniel

 

Dag Daniël,

Zo te zien heb je gelijk. 
Welke fout zou het antwoordenboek gemaakt kunnen hebben? 
(Want tussen jouw antwoord en het hunne  zit wel een opvallend precieze factor 2 verschil.)

Groet, Jan

Zoals je zegt:

T = 3 s dus L = 2,24 m

Maar dan sin α = 0,01/L (alles in meter) --> α = sin^-1 0,01/L

tan α = h/0,01 --> h = 0,01 tan α = 0,01 tan sin^-1 0,01/L --> 0,01 * 4,46 * 10^-3 = 4,6 * 10^-5 m

E = mgh = 5,0 * 9,81 * 4,6 * 10^-5 = 2,2 * 10^-3 J 

En dat is niet het antwoordenboekje-antwoord. Dat zou er ook wel eens naast kunnen zitten. Een drukfout zou niet voor het eerst zijn.

Dag allen,

a. In Theo's rechter figuur is h langs de verticaal door het ophangpunt van de slinger en is 1 cm horizontaal, loodrecht op h. Zodoende lijkt de figuur 'onderste boven'. Dat mag natuurlijk.
Theo's rechter figuur komt dan overeen met de driehoek FGH in de onderstaande tekening. Het 'dak' van Theo's figuur is een rechte lijn die overeenkomt met de raaklijn FG hieronder. Is Theo's figuur zo bedoeld?
Dan is h in Theo's figuur (HG hieronder) niet de hoogte van de slingerende massa boven de evenwichtsstand en niet de hoogte $h$ die we moeten invullen in de formule $E_\text{pot}=m\cdot g\cdot h$. Dit verklaart het verschil tussen Daniels uitkomst en het antwoordenboek.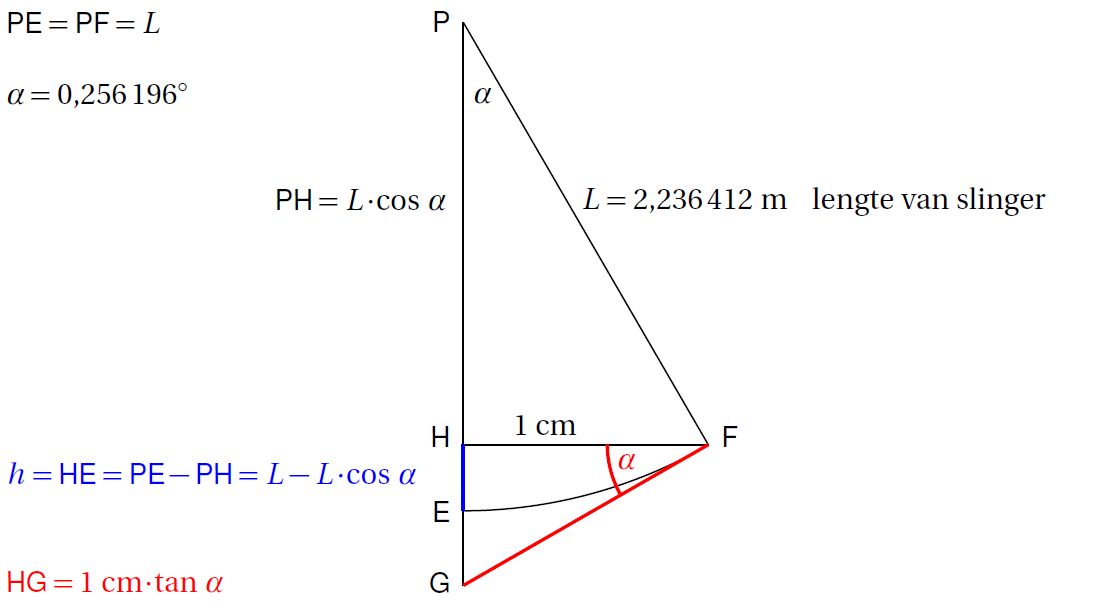



De hoogte $h$ voor $E_\text{p}=m\cdot g\cdot h$ is HE=PE-PH in mijn tekening.
Want de massa beweegt langs de cirkelboog EF.

Bij het ophangpunt geldt

De zijde PH is

De hoogte van de slingerende massa boven de evenwichtsstand is

De potentiële energie bij een horizontale uitwijking van $0,01\,\text{m}$ is

Bij deze kleine $\alpha$ is h uit Theo's rechter figuur een factor 2 maal te groot, zoals we wiskundig kunnen aantonen in de limiet voor $\alpha$ nadert tot nul. Het is geen kwestie van afronden of zoiets.

b. Volgens Jan zijn de formules die Henry gebruikt, niet geldig voor de slinger. Maar bij de kleine $\alpha$ van deze opgave kun je de beweging langs de cirkelboog in goede benadering wel degelijk beschrijven met Henry's formules voor een harmonische trilling. We noemen $k$ dan niet de veerconstante maar de krachtconstante. Het is de evenredigheidsconstante in


c. Henry's berekening is in wezen goed. Hij maakt alleen een rekenfout:

waarna inderdaad $E_\text{p}=0,0011\,\text{J}$.

d. Het kan ook korter.
Voor een harmonische trilling, en in goede benadering ook voor deze slinger, geldt


e. Theo noteert om 17.32 uur: '0,01 * 4,46 * 10^-3= 4,6 * 10^-5 m'
Maar 0,01*4,46*10^-3=4,46*10^-5 m, zoals Daniel al schreef in cm, zonder tussendoor afronden.
Groet, Jaap

> 4,46 * 10^-3 = 4,6 * 10^-5 m

Inderdaad eeb "4" weggevallen. Slordig.