Dag Mourad,

Metingen zijn altijd onnauwkeurig, zoals je opmerkt. Dat doet niks af aan het feit dat een v/t verband voor een vrij vallend balletje in theorie rechtevenredig is. 
Jouw taak om in een foutendiscussie te proberen de gemeten afwijkingen te verklaren.

Ik heb een paar punten van kritiek op jouw wijze van grafieken tekenen:

1. gebruik liefst hele "liniaal"getallen bij de assen, dwz 1,2 of 5, of tienvouden daarvan. Op de verticale as doe je dat goed, op de horizontale laat dat te wensen over.
2. Gebruik +jes om je getallenparen in te tekenen. Afhankelijk van de geschatte (on)nauwkeurigheid van je metingen maak je die +jes groter of kleiner
3. Teken geen geknikte grafieklijnen voor natuurlijke processen; op macroschaal verlopen die NOOIT in plotselinge stapjes zoals jouw knikken lijken te suggereren. 
4. De rode lijn teken je zelfs liefst helemaal niet, ook niet met vloeiende bochten. 
5. De zwarte lijn tekende je van eerste naar laatste punt: zijn die meer waard dan de tussenliggende? 

Ten slotte mogen we ons afvragen of een vallend balletje zoals je dat meet, in een omgeving waar luchtweerstand ook een rol zal beginnen spelen bij oplopende snelheden, nog wel aan een rechtevenredig v/t verband zal mogen voldoen. 

Als je dit (val)proefje in vacuüm uitvoert, in principe wél ja.

Groet, Jan

Bedankt,
ik snap punt 5 en 6 niet helemaal. de rode lijn zijn gewoon de meetwaarden en de driehoek is de oppervlakte onder de grafiek (hij is negatief dus hij moet erboven). Bedankt voor de rest!

Meetwaarden die, zoals je zelf ook al constateert, zoals alle meetwaarden een beperkte nauwkeurigheid kennen. De werkelijke grafiek is dan een VLOEIENDE lijn die zeker niet per se door elk punt gaat,  maar een logisch verwacht verloop kent langs een soort van gemiddelde van meetpuntplaatsen.

zoals bijvoorbeeld de grafiek in onderstaand diagram: 


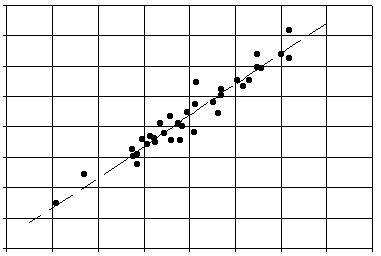
Zoiets zou jouw grafiek ook worden als je hetzelfde experiment een aantal keren herhaalt. Elk punt op zich betekent weinig, maar sámen beteken ze veel meer. Niemand die hier lijntjes gaat trekken van punt naar punt naar punt toch? 

Jij hebt veel minder punten uit dit ene experiment. Beter teken je je grafiek dus als zoiets:

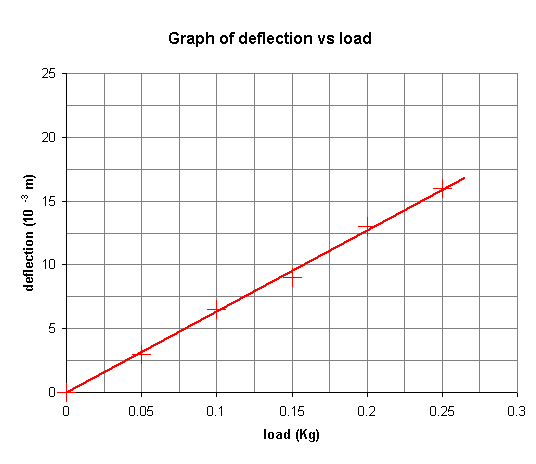
De horizontale en verticale lijntjes (samen +jes) symboliseren een schatting van hoe ver de werkelijke waarden redelijkerwijs kunnen hebben afgeweken van de gemeten waarden, de grafieklijn is een conclusie van het meest waarschijnlijke verloop van de werkelijke waarden. De meetpunten zijn evenwichtig verdeeld onder en boven de geschatte lijn.
Een kronkellijn is al onwaarschijnlijker, eentje met knikjes een grafiek die de waarheid zéker ernstig geweld aandoet: jouw balletje zal tussen 0,12 en 0,24 s vast niet een meer dan 2 x zo grote versnelling gekend hebben dan tussen 0 en 0,12 s, (zie helling van jouw rode grafiek op die intervallen),  laat staan dat die versnelling PLOTS verdubbelde op t= 0,12 s. 

Jouw zwarte lijn is dus een héél wat betere benadering van de werkelijkheid dan die rode.punt 6? 

Groet, Jan

4 en 5 bedoelde ik.... 

wat betreft punt 5: het kán toeval zijn, of een verschil van inschatting tussen jou en mij. Maar ik zie je een lijn trekken van de oorsprong naar je laatst gemeten punt. Dat doe je om een oppervlak te schatten onder je rode grafiek.

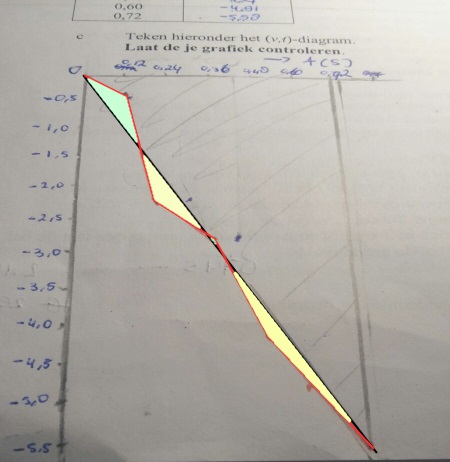
Niet dat die rode grafiek eigenlijk enige waarde heeft, maar als je hem wél als waardevol zou beschouwen (zoals je nog deed toen je die zwarte lijn trok nog voor we aan deze topic begonnen) dan zien we dat door die zwarte lijn zó te trekken er meer oppervlak buiten je zwarte lijn wegvalt (geel) dan je er binnen je zwarte lijn voor terugpakt (groen) .



persoonlijk vermoed ik overigens dat een serie herhalingen van je experiment zou leiden tot ongeveer zo'n grafiek:



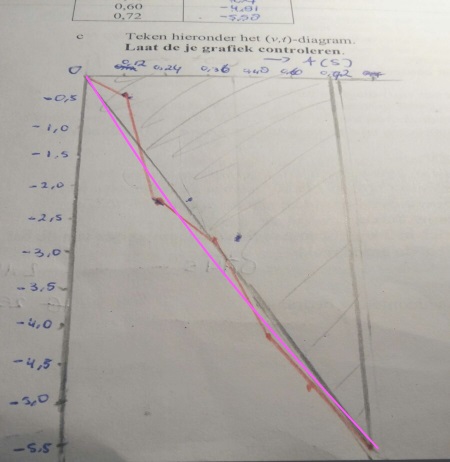
waarbij we een lichtjes afnemende versnelling zien a.g.v. toenemende luchtweerstand en dus afnemende nettokracht.
Een kromme v/t grafiek dus, die steeds vlakker gaat verlopen.

Groet, Jan

Ja de docent heeft die oppervlakte getekend, ik twijfelde ook toen ik nog eens naar het practicum keek... verder hadden we geen tijd om meerdere metingen uit te voeren dus dit zijn de enige meetwaarden die ik heb. Ik heb na uw advies wel de knikjes weggehaald en er een kromme van gemaakt.

alleen nog wel een verklaring proberen te vinden voor die toch wel enorme uitbijter bij 0,12 s. 
daar verwachten we theoretisch een snelheid van v= a·t = 9,8 x 0,12 ≈ 1,18 m/s.
Jouw punt staat nog niet eens op de helft daarvan. Hoe kom je aan die snelheden, hoe heb je die gemeten??

Uit de rest van de gegevens blijkt overigens ook een verre van vrije val: na 0,72 s verwachten we een snelheid van ca 7 m/s, jij vindt "maar" 5,6 m/s. 
Een of ander licht, plastic balletje ipv een stalen kogel? Des te meer reden om een kromme te veronderstellen.

Het was een pingpongballetje. Aangezien het een videometing was en het aantal fps niet aanzienlijk hoog was kan het waarschijnlijk daar aan liggen

des te meer reden om zeker geen rechte te tekenen :)

dat durf ik van hieruit niet te beoordelen, maar klinkt plausibel. Nóg meer reden om geen rode zigzaglijn langs je onbetrouwbare meetpunten te gaan tekenen.

Hier hebben ze het met wat betere apparatuur dan jij gedaan:

https://met213.tech.purdue.edu/French/Example%20Problems/Ping%20Pong%20Ball%20Drop%20-%20Published%20Article.pdf

als je de v/t grafiek die ze daar maakten vergelijkt met die van jou (moet je uiteraard wel spiegelen)  dan zie je dat er tussen 0,3 en 0,7 seconden toch al een forse bocht in begint te komen. 

groet, Jan

bedankt voor alles !! Zal de tips zeker onthouden voor een volgend practicum

graag gedaan en succes verder