Reacties
Jan van de Velde
op
22 november 2020 om 15:34
dag Liza,
Ik snap dat ook niet.
wet van behoud van energie luidt:
optelsom van alle veranderingen van alle denkbare betrokken vormen van energie = 0
dus bij een bal die je in vacuüm laat vallen geldt ΔEz + ΔEk = 0
en dat zou je dan kunnen herschrijven tot ΔEz = -ΔEk
maar niet tot ΔEz = -2ΔEk.
Dus: wie of wat vraagt je om dat aan te tonen? Context?
groet, Jan
Ik snap dat ook niet.
wet van behoud van energie luidt:
optelsom van alle veranderingen van alle denkbare betrokken vormen van energie = 0
dus bij een bal die je in vacuüm laat vallen geldt ΔEz + ΔEk = 0
en dat zou je dan kunnen herschrijven tot ΔEz = -ΔEk
maar niet tot ΔEz = -2ΔEk.
Dus: wie of wat vraagt je om dat aan te tonen? Context?
groet, Jan
Lisa
op
22 november 2020 om 15:40
Het zit in een oefentoets (van mijn docent) over hemelmechanica (vwo 5)
ik moet aantonen dat:
mgh = -2(½mv²)
Alleen kom ik niet verder dan:
mgh = -mv²
gh = -v²
ik moet aantonen dat:
mgh = -2(½mv²)
Alleen kom ik niet verder dan:
mgh = -mv²
gh = -v²
Hans
op
22 november 2020 om 15:46
Is dit misschien zo bij een bal die omhooggegooid wordt? Als hij weer op het startpunt uitkomt?
Hans
op
22 november 2020 om 15:48
2 x 1/2 = 1
Theo de Klerk
op
22 november 2020 om 15:51
Wat stelt in hemelmechanica "h" voor in mgh????? mg is normaal de aantrekkingskracht van de aarde op iets vlak boven (h <1 km) aarde als je g constant mag verwachten.
Heeft het iets met ontsnappingssnelheid te maken? Dan is g = GMaarde/r2 en verandert steeds van waarde omdat r verandert.
Kun je de complete letterlijke (niet eigen interpretatie!) opgave eens geven?
Heeft het iets met ontsnappingssnelheid te maken? Dan is g = GMaarde/r2 en verandert steeds van waarde omdat r verandert.
Kun je de complete letterlijke (niet eigen interpretatie!) opgave eens geven?
Jan van de Velde
op
22 november 2020 om 15:52
Moet je dat zomaar "kaal" aantonen? Geen context? Raar.
Hoe dan ook, ik zie niet hoe die bewering überhaupt zou kloppen. Ik kan er geen natuurkundige situatie bij bedenken zo gauw.
Wat je op zijn best kunt doen is laten zien dat de vergelijking wel dimensioneel (d.w.z. qua eenheden) klopt. Dus voor g de m/s² invullen etc, en dan kijken of je alles tegen elkaar kunt wegstrepen.
Hoe dan ook, ik zie niet hoe die bewering überhaupt zou kloppen. Ik kan er geen natuurkundige situatie bij bedenken zo gauw.
Wat je op zijn best kunt doen is laten zien dat de vergelijking wel dimensioneel (d.w.z. qua eenheden) klopt. Dus voor g de m/s² invullen etc, en dan kijken of je alles tegen elkaar kunt wegstrepen.
Lisa
op
22 november 2020 om 15:58
Kun je de complete letterlijke (niet eigen interpretatie!) opgave eens geven?
Lisa
op
22 november 2020 om 16:02
Hans Hokke plaatste:
Is dit misschien zo bij een bal die omhooggegooid wordt? Als hij weer op het startpunt uitkomt?
Arno
op
22 november 2020 om 16:04
Lisa plaatste:
Toon aan dat Ez = -2Ek. Gebruik hierbij Fg = Fmpz
Lisa
op
22 november 2020 om 16:09
Arno van Asseldonk plaatste:
Het gaat dus blijkbaar om een eenparige cirkelvormige beweging. Kun je misschien de rest van de opgave er ook eens bij zetten?Dit is helaas de hele opdracht, er is verder geen context of waardes die we moeten invullen: het gaat dus ook niet om een bepaald hemellichaam.
Het gaat om een algemene cirkelvormige baan.
Lisa
op
22 november 2020 om 16:17
Tot nu toe heb ik
Fg = Fmpz
GmM/r² = mv²/r
GmM/r = mv²
En ik moet uitkomen op
Ez = -2Ek
mgh = -2(½mv²)
mgh = -mv²
Fg = Fmpz
GmM/r² = mv²/r
GmM/r = mv²
En ik moet uitkomen op
Ez = -2Ek
mgh = -2(½mv²)
mgh = -mv²
Theo de Klerk
op
22 november 2020 om 16:24
Ahh.... wat een gluiperds!
g = GM/r2 dus gr = GM/r = v2 (volgens wat Lisa al eerder afleidde).
Maar "g" is hier g(r) = GM/r2 en hun helemaal niet constant.
Maar voor een hoogte (vanuit middelpunt aarde) r is die te berekenen als g = GM/r2
Dan geldt m(GM/r2)r = m g h = mv2
waarbij g dus niet 9,81 m/s2 is maar de waarde die hoort bij de gegeven r.
Overigens is "h" dan ook niet de hoogte, maar de baanstraal (hoogte = r - Raarde)
g = GM/r2 dus gr = GM/r = v2 (volgens wat Lisa al eerder afleidde).
Maar "g" is hier g(r) = GM/r2 en hun helemaal niet constant.
Maar voor een hoogte (vanuit middelpunt aarde) r is die te berekenen als g = GM/r2
Dan geldt m(GM/r2)r = m g h = mv2
waarbij g dus niet 9,81 m/s2 is maar de waarde die hoort bij de gegeven r.
Overigens is "h" dan ook niet de hoogte, maar de baanstraal (hoogte = r - Raarde)
Lisa
op
22 november 2020 om 16:34
ooh dus
g = GM/r²
r = h
waardoor
mgh = m(GM/r²)r
Heel erg bedankt voor de hulp!! :)
g = GM/r²
r = h
waardoor
mgh = m(GM/r²)r
Heel erg bedankt voor de hulp!! :)
Jan van de Velde
op
22 november 2020 om 17:06
Niks voor Lisa om zich wat van aan te trekken, maar ik zie nog steeds de natuurkundige betekenis van deze vergelijking niet.
mgr mag ik volgens mij niet gelijkstellen aan Ez, omdat tijdens stijgen of dalen (over significante afstanden) die g helemaal niet constant blijft, en ook niet lineair toe- of afneemt, zodat die factor "2" ook niet die g ter hoogte van de baan kan omzetten in een afstands-gemiddelde g over de potentiële valhoogte.
mgr mag ik volgens mij niet gelijkstellen aan Ez, omdat tijdens stijgen of dalen (over significante afstanden) die g helemaal niet constant blijft, en ook niet lineair toe- of afneemt, zodat die factor "2" ook niet die g ter hoogte van de baan kan omzetten in een afstands-gemiddelde g over de potentiële valhoogte.
Arno
op
22 november 2020 om 17:45
Ik denk dat we hier uit moeten gaan van Ez = -GmM/r en niet van de formule voor de energie van een massa m op hoogte h.
Theo de Klerk
op
22 november 2020 om 18:13
Klopt. De Ezw is door de steeds wijzigende grootte van g uiteindelijk (na integratie) gelijk aan -GM/r en dat is wiskundig wel gelijk aan - g (=GM/r2) maal r.
Dus de vergelijking zou dan moeten zijn mgh = - mv2 Al hangt dat minteken af van begin- en eindwaarde van de integratie (van oneindig naar 0 is het +, van 0 naar oneindig is het - )
Dus de vergelijking zou dan moeten zijn mgh = - mv2 Al hangt dat minteken af van begin- en eindwaarde van de integratie (van oneindig naar 0 is het +, van 0 naar oneindig is het - )
Jaap
op
25 november 2020 om 22:10
De valversnelling g kan verwarring geven. Daarom vermijden we g. Hieronder is G de gravitatieconstante.
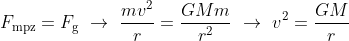
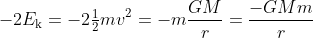
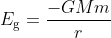
zodat
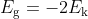
Bij zo'n cirkelbaan schrijven we vaak gravitatie-energie in plaats van zwaarte-energie.
zodat
Bij zo'n cirkelbaan schrijven we vaak gravitatie-energie in plaats van zwaarte-energie.
