Al dik 30 jaar zijn fysici bezig om de algemene relativiteitstheorie (ART) en de Quantum Mechanica (QM) te verenigen tot één theorie: de snaartheorie. Aan de Rijksuniversiteit in Groningen (RUG) wordt ook druk aan deze theorie gewerkt. Wat houdt nou precies die snaartheorie in, en waarom is het zo lastig om de ART en de QM te verenigen? En bovenal, waar is het goed voor?
De algemene relativiteitstheorie (ART)
In 1916 heeft Einstein zijn vindingen gepubliceerd over hoe zwaartekracht nou precies werkt. Deze theorie is de algemene relativiteitstheorie. In het kort zegt de theorie dat zwaartekracht een gevolg is van de kromming van de ruimtetijd. Dat betekent: hoe meer energie en massa er aanwezig is, des te meer is de ruimtetijd gekromd. Voor zwakke zwaartekrachtsvelden komt de ART overeen met de Newtoniaanse mechanica, maar voor een juiste beschrijving heb je voor sterkere velden echt de ART nodig.
In de literatuur wordt vaak een analogie gemaakt met een knikker op een stuk papier. De knikker zal het papier krommen, en hoe zwaarder de knikker, des te meer wordt het papier gekromd. Het papier komt hier dan dus overeen met de ruimtetijd, en de kromming met de zwaartekracht.
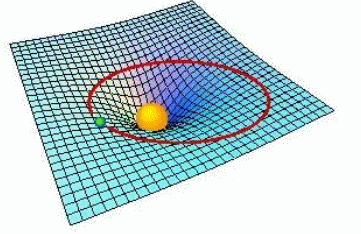
Het pad van een object wordt bepaald door de kromming van de ruimtetijd. De ART voorspelt dus ook dat de ruimtetijd niet gekromd zal zijn, als er geen massa en energie is. Nou is zwaartekracht een kracht die vooral op grote schaal merkbaar is; op atomair niveau is ze verwaarloosbaar klein. Je kunt dus stellen dat de ART je vertelt hoe het universum er uitziet op grote schaal.
Intermezzo relativiteitstheorie: speciaal en algemeen
De algemene relativiteitstheorie is een uitbreiding van de speciale relativiteitstheorie. De speciale theorie gaat uit van de waarneming dat licht constant is. Daaruit volgt dat ruimte en tijd gekoppeld zijn. Ze zijn te verenigen tot één verzameling: de ruimtetijd. Deze ruimtetijd is dus een 4-dimensionale verzameling. Elk punt bestaat uit 3 plaatscoördinaten en 1 tijdscoördinaat. Zo’n punt kun je dan voorstellen als {ct,x,y,z}. Om alle componenten dezelfde grootheid te geven, neem je vaak c*t in plaats van t, waarbij c de lichtsnelheid is. Deze is immers toch constant!
De speciale relativiteit gaat grotendeels over wat er gebeurt als waarnemers met hoge snelheden gaan reizen. Bepaalde grootheden, zoals massa, tijd en lengte worden dan afhankelijk van de waarnemer. Maar de speciale relativiteitstheorie omvat geen zwaartekracht. Het heeft Einstein 10 jaar van zijn leven gekost om de speciale theorie uit te breiden naar een algemene, die ook de zwaartekracht omvat. Zijn briljante ingeving (of, zoals hij het zelf noemde, zijn “eurekamoment”) was dat je zwaartekracht kon zien als een kromming van de ruimtetijd. Een object bezit massa en energie en dit kromt de ruimtetijd. Wij ervaren dat vervolgens als zwaartekracht.
Merk hier op dat je dus niet over zwaartekrachtsdeeltjes spreekt.
Het idee, dat zwaartekracht door bepaalde deeltjes wordt overgebracht is een wens van de quantum mechanica (QM). De QM behandelt materie en krachten in termen van deeltjes en golven. In dat opzicht is zwaartekracht dus erg anders dan andere krachten. Zwaartekracht is de enige kracht die de ruimtetijd beïnvloedt; de andere krachten doen dat niet.
De quantum mechanica (QM)
Op kleine schaal heb je een andere theorie, de QM. Deze voorspelt onder andere dat deeltjes niet alleen door deeltjeseigenschappen kunnen worden beschreven, maar dat zo’n deeltje ook golfeigenschappen heeft. Dat lijkt vreemd, want deeltjes en golven zijn twee compleet verschillende dingen. Toch blijkt deze beschrijving erg goed te werken. Het geeft onder andere een verklaring voor het "2-spleten" experiment. Eén gevolg van deze deeltjesgolfdualiteit: bepaalde grootheden van een deeltje kun je nooit allebei tegelijkertijd exact meten. Dit heet het onzekerheidsprincipe van Heisenberg. Op zeer kleine schaal kunnen deeltjes worden gecreëerd en weer vernietigd. Dat voorspelt het onzekerheidsprincipe. Zolang de tijdsduur van dit proces kort genoeg is, kun je als het ware energie “lenen” uit het niets. Als het maar weer op tijd wordt “terugbetaald”.
Onzekerheidsprincipe van Heizenberg. Hoe preciezer je de ene grootheid meet, des te meer onzekerheid krijg je in de andere. Dit geldt onder andere voor de energie en de tijd, maar bijvoorbeeld ook voor de plaats en de impuls van een deeltje.
Intermezzo quantum mechanica (QM)
De QM is in de jaren 20 van de vorige eeuw ontwikkeld. Deze theorie gaat ervan uit dat deeltjes zich ook als golven gedragen, en dat grootheden als energie gequantiseerd zijn in plaats van continu. Het golfkarakter van zo’n deeltje wordt beschreven door de formule van de Broglie. Nou kun je van een deeltje heel goed de plaats meten, maar een golf is “uitgesmeerd” en kent geen goed gedefinieerde positie. Dit resulteert in het onzekerheidsprincipe. Het onzekerheidsprincipe van Heisenberg is een erg belangrijk principe. Het beweert dat je altijd een onzekerheid zult hebben in je meting als je bepaalde grootheden tegelijkertijd meet. Een voorbeeld hiervan is de plaats x en de impuls p. Heisenberg zegt hierover:
Δx*Δp> ħ
- Δ is hier een onzekerheid in de grootheid
- ħ is de constante van Planck, gedeeld door 2π
Je ziet dus, dat als de onzekerheid in x afneemt, de onzekerheid in p moet toenemen en vica versa. Dit geldt ook voor de energie en de tijd:
ΔE*Δt> ħ
Eén interpretatie hiervan is, dat je zogenaamde “imaginaire deeltjes” kunt krijgen vanuit het niets. Zo’n imaginair deeltje is niet rechtstreeks te meten, maar de invloeden ervan zijn wel degelijk te meten! Wat bovenstaande formule eigenlijk zegt, is dat hoe meer energie zo’n imaginair deeltje heeft, des te korter kan het bestaan. Er is immers toch een bepaalde onzekerheid over de twee grootheden! Op deze manier kan in het vacuüm op erg kleine schaal een constant proces van creatie en vernietiging van deeltjes plaatsvinden. Hierbij is de gemiddelde energie dan natuurlijk wel 0. De wet van behoud van energie wordt dus niet geschonden.
Waar de QM en ART elkaar tegenspreken
Nu komt het cruciale: de ART zegt dat in een lege ruimtetijd de ruimtetijd volledig vlak is, hoe ver je ook inzoomt. Er is immers geen energie aanwezig. Maar de QM vertelt je, dat er op heel kleine schaal constant deeltjes worden gecreëerd en vernietigd. En deze deeltjes hebben toch invloed op de ruimtetijd! Hoewel die deeltjes maar heel kort bestaan, krommen ze op erg kleine schaal de ruimtetijd aanzienlijk.

Op dit niveau wordt de ruimtetijd door beide theorieën afzonderlijk niet meer goed beschreven. En dus is er een vereniging nodig.
Van punten naar snaren
De QM behandelt deeltjes als punten zonder afmetingen, en dus zonder innerlijke structuur. De snaartheoretici bedachten dat op zeer kleine schaal die deeltjes misschien wel snaartjes zijn, en dus toch een structuur zouden hebben.
Op grote schaal merk je weinig van die snaareigenschappen, maar op kleine schaal wordt deze structuur belangrijk. Het idee is dat de manier waarop zo’n snaar trilt, de deeltjeseigenschappen bepaalt, zoals de massa. Toen dit werd uitgewerkt, bleken er twee opmerkelijke eigenschappen te zijn van dit model:
- Er was een deeltje in het model bijgekomen, wat precies de eigenschap had die je verwacht van een zwaartekrachtsdeeltje (het zogenaamde graviton).
- Om de vergelijkingen kloppend te maken, had je meerdere ruimtelijke dimensies nodig.
In dit model wordt de zwaartekracht kennelijk als een deeltje weergegeven, in plaats van de manier waarop de ART de zwaartekracht beschrijft. Dit model omvat dus zowel de QM als de ART! Alleen bleken die extra dimensies een probleem te zijn. Het aantal manieren waarop je deze in je model kon stoppen was reusachtig groot. Tot op de dag van vandaag zijn fysici bezig om deze, en andere complicaties, weg te werken. Maar als de snaartheorie juist blijkt te zijn, dan zijn er dus extra ruimtelijke dimensies: in totaal 9, om precies te zijn. In het dagelijks leven heb je maar te maken met 3, en geen 9. Dit kun je verklaren aan de hand van de grootte van de dimensies. Deze zijn zo klein, dat je heel ver moet inzoomen wil je de structuur ervan zien.

Op grote schaal lijkt een stukje ruimtetijd 4-dimensionaal (dat zegt de ART ook). Maar op kleine schaal vind je dan meer “opgerolde” dimensies.
Het nut van de snaartheorie
Zo op het eerste gezicht lijkt de snaartheorie erg exotisch, en dat is het ook. In het dagelijkse leven heb je weinig te maken met de verschijnselen die deze theorie voorspelt. Maar er zijn wel situaties waar de snaartheorie nodig is. Voorbeelden zijn zwarte gaten, die erg zwaar zijn, en een beschrijving van het universum net na de oerknal. Dit zijn twee extreme situaties, waarbij je een theorie nodig hebt die zowel op grote als op kleine schaal nuttige uitspraken doet.
Conclusie
Nu weet je waar de twee theorieën elkaar tegenspreken. En hopelijk is het duidelijk geworden waarom er zo druk naar een theorie wordt gezocht die de QM en de ART verenigt. Is de snaartheorie de juiste theorie hiervoor? Dat is nog niet te zeggen. Maar het is op dit moment de meest aantrekkelijke kandidaat voor een theorie die alle krachten verenigt.
